Written by J.A Dobado | Last Updated on May 2, 2024
What is the Nernst’s distribution law?
The Nernst’s distribution law (or Nernst’s partitioning law) was enunciated by the, Nobel prize in 1920, German physical chemist Walther Hermann Nernst (1864–1941), and explains how a solute will be distributed between two immiscible solvents. It is a concept widely used in solutions of immiscible liquids.
If we have two non-miscible solvents and we add a solute to them, this will be distributed between them in such a way that it is fulfilled that:
“the ratio between solute concentrations (C) in the two non-miscible liquids is going to be a constant, independent of the amount of solute added, and equal to the ratio between their respective solubilities (S).“
The ratio of its concentrations in the two solvents is constant, and is described by the relation:
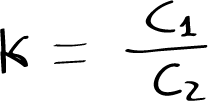
where C1 and C2 are, respectively, the amount of substance concentrations of the solute in solvent 1 and 2 at equilibrium, and K is the distribution constant. The law only applies in dilute solution.
Examples
Iodine I2 is approximately 85 times more soluble in carbon tetrachloride CCl4 than in water H2O, or in other words, we can have the same amount of iodine in water as in 85 times less carbon tetrachloride CCl4.
This property allows us to extract all the I2 from H2O using CCl4. This process is called extraction.
How is greater efficiency achieved in an extraction process?
- Increasing the number of extractions.
- Making the volumes used of the extracting solvent (CCl4) as small as possible.
Therefore, the partition coefficient of A between S1 and S2 is 2/3 and the distribution coefficient of A is 0.4.
Exercise
A solute A is distributed between two solvents S1 and S2 in the ratio of 2:3 at a given temperature. Calculate the partition coefficient D and the distribution coefficient of the solute between the two solvents.
Solution:
According to Nernst’s distribution law, the ratio of the concentrations of the solute in two immiscible solvents is a constant at a given temperature. This constant is called the partition coefficient (K) of the solute between the two solvents.
K = [A]S1 / [A]S2
where [A]S1 and [A]S2 are the concentrations of the solute in solvents S1 and S2, respectively.
In this case, the ratio of the concentrations of A in S1 and S2 is 2:3. Let’s assume that the initial concentration of A is x. Therefore, the concentration of A in S1 is 2x/5 and the concentration of A in S2 is 3x/5. The total ammount of solvent is 5.
So, the partition coefficient K of A between S1 and S2 is:
K = (2x/5) / (3x/5) = 2/3
The distribution coefficient (D) is defined as the ratio of the amount of solute distributed in one solvent to the total amount of solute distributed in both solvents.
D = (amount of A in S1) / (amount of A in S1 + amount of A in S2)
Let’s assume that the total amount of A distributed in both solvents is 1 mole. Then, the amount of A distributed in S1 is (2/5) mole and the amount of A distributed in S2 is (3/5) mole.
So, the distribution coefficient of A is:
D = (2/5) / [(2/5) + (3/5)] = 0.4
Limitations of Nernst’s distribution law
Nernst’s distribution law is a powerful tool for predicting the distribution of a solute between two immiscible solvents. However, there are certain limitations to this law that should be kept in mind:
- Only applicable to non-electrolytes: Nernst’s distribution law is only applicable to non-electrolytes, which are molecules that do not ionize in solution. Electrolytes, which are substances that dissociate into ions in solution, have a more complex distribution behavior that cannot be predicted by Nernst’s law.
- Assumes equilibrium conditions: Nernst’s distribution law assumes that the system has reached equilibrium. In reality, many systems are far from equilibrium, and the actual distribution of a solute may be affected by factors such as kinetics, adsorption, and diffusion.
- Assumes ideal solutions: Nernst’s distribution law assumes that the solvents are ideal solutions, which means that their properties such as density, viscosity, and surface tension do not vary with composition. However, in real solutions, these properties can change significantly with composition, which can affect the distribution of a solute.
- Limited to dilute solutions: Nernst’s distribution law is applicable only to dilute solutions, where the concentration of the solute is much lower than the concentration of the solvents. In concentrated solutions, the distribution behavior can be significantly affected by factors such as solute-solute interactions and the formation of complexes.
- Does not account for solute-solvent interactions: Nernst’s distribution law assumes that the solute molecules do not interact with the solvent molecules, which is not always true. In some cases, the solute-solvent interactions can affect the distribution behavior, and this cannot be predicted by Nernst’s law.
References
Nernst, W. (1891). “Verteilung eines Stoffes zwischen zwei Lösungsmitteln und zwischen Lösungsmittel und Dampfraum“. [Distribution of a substance between two solvents and between solvent and vapor space.] Zeitschrift für Physikalische Chemie. 8U (1): 110–139. DOI: 10.1515/zpch-1891-0806