Written by J.A Dobado | Last Updated on April 22, 2024
Basic concepts
Many organic molecules have the peculiarity of having the same molecular formula, but different physicochemical properties, receiving the name of isomers. The following scheme summarizes the types of isomerism characteristic of organic molecules:
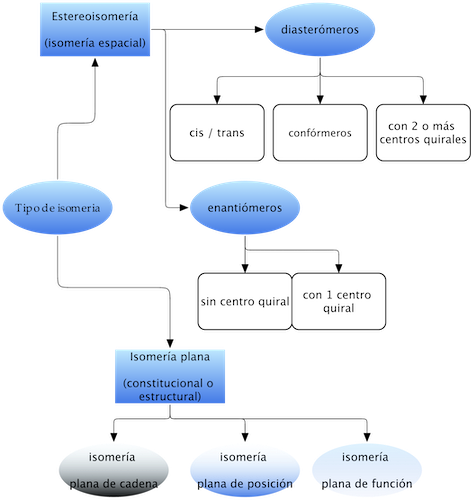
Planar isomerism (constitutional or structural)
Planar isomers differ in their connectivity (the way in which atoms are bonded together), and these differences become apparent when we represent them in the plane. They are classified into three types:
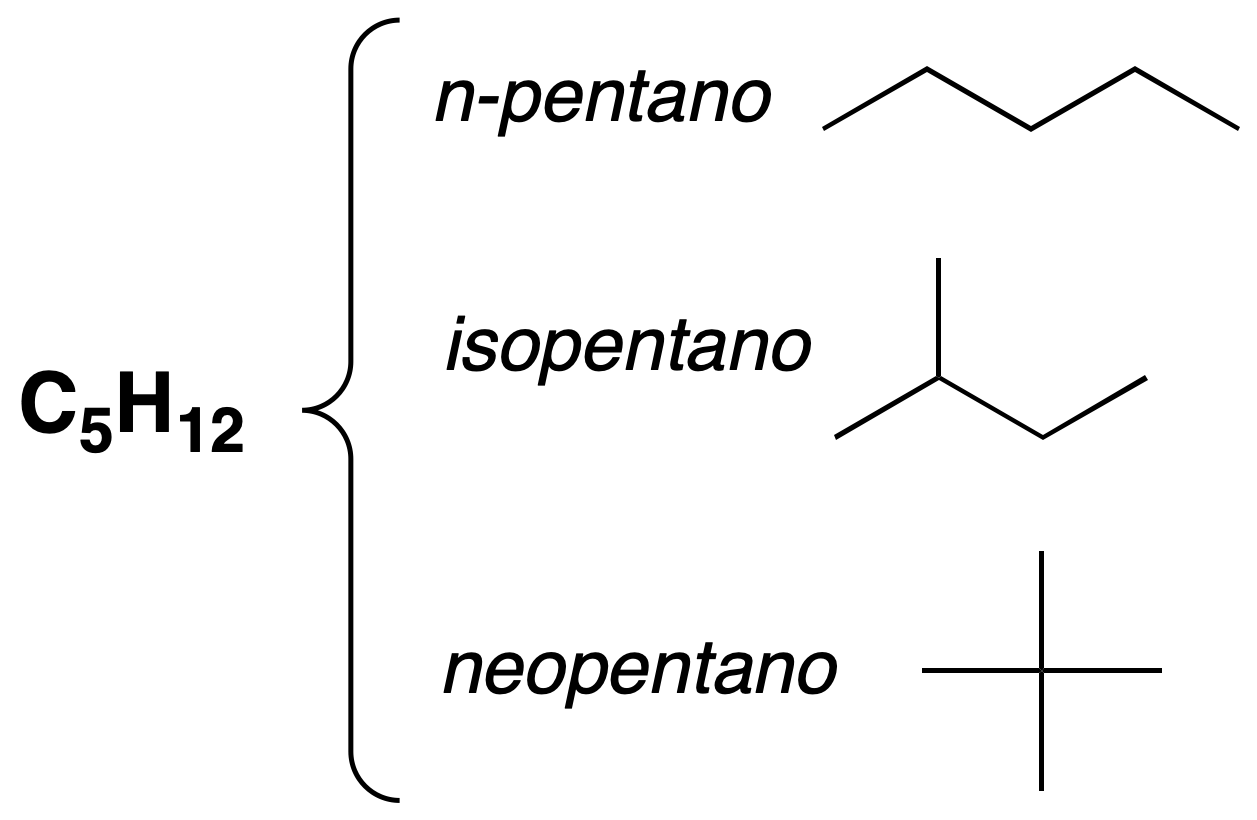
Chain isomerism
They have different main chain.
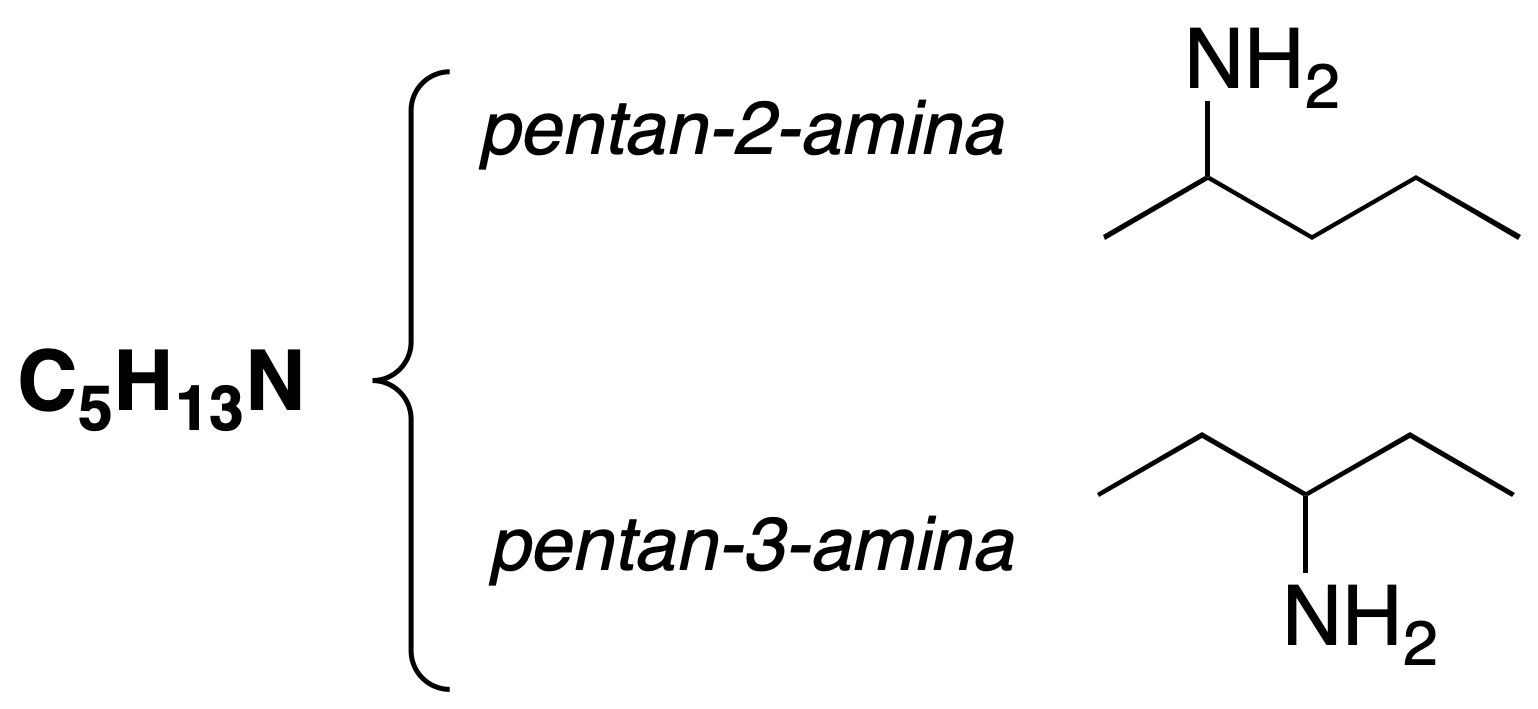
Position isomerism
The position of the functional group in the chain is different.
Function isomerism
These isomers have different functional groups.
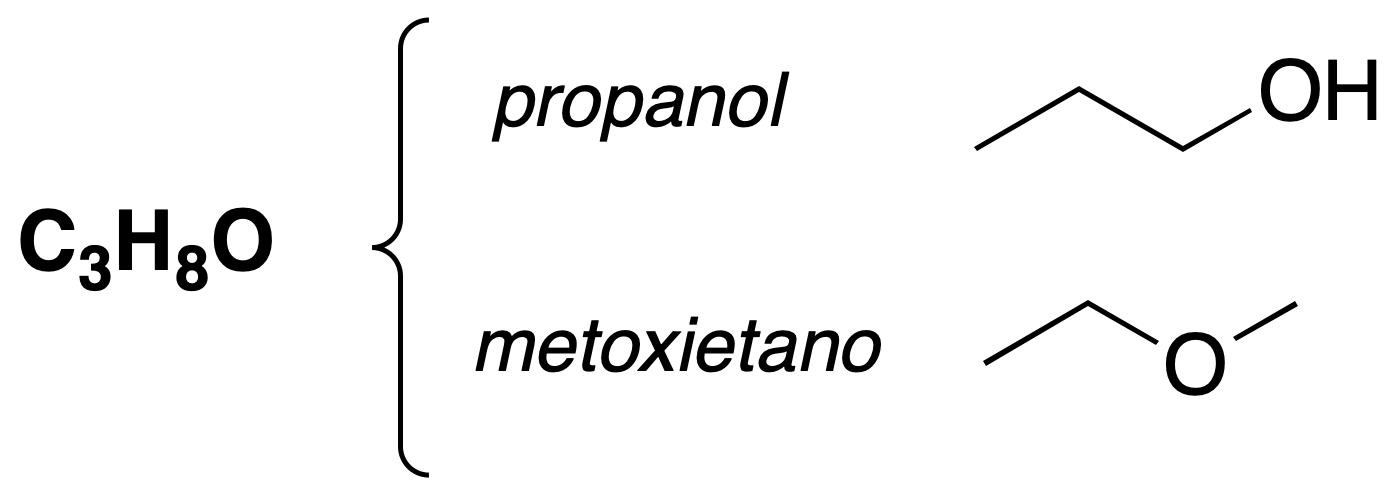
Stereoisomerism (spatial isomerism)
These isomers have the same connectivity (same number and type of bonds), but differ in their configuration (the way their atoms are oriented in space). The grouping responsible for stereoisomerism is called a stereogenic unit.
There are two types of stereoisomers:
Enantiomers
Diasteromers
Two stereoisomers that are not mirror images. They are subdivided into:
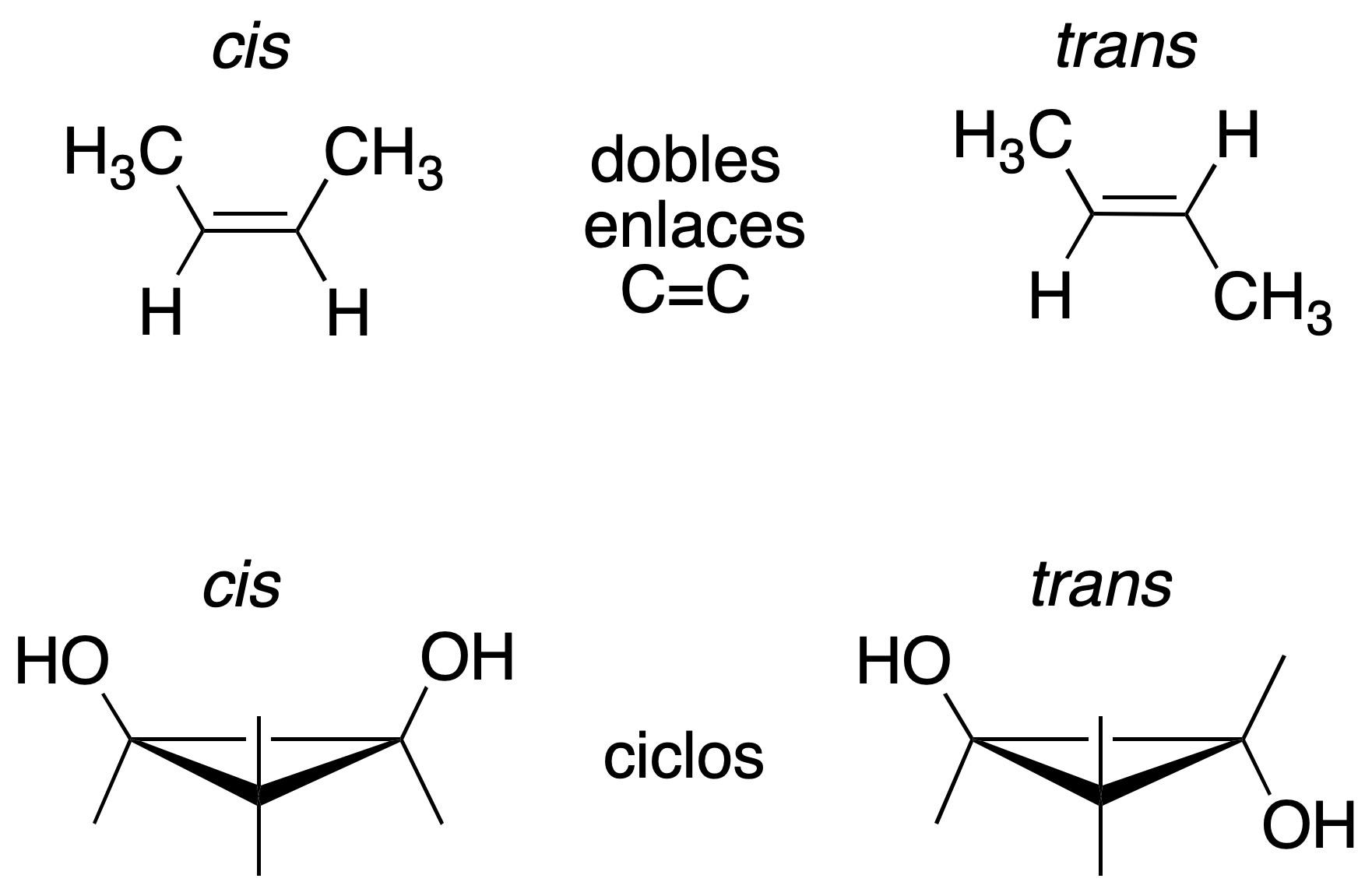
cis-trans isomerism
When such isomers cannot be interconverted by rotation into bonds. Two groupings of atoms attached to each of the carbons with a double bond, or ring, that differ in positions with respect to the reference plane of the double bond or ring.
Conformational isomerism
When such isomers can be interconverted by rotation around single bonds, with more or less restrictions.
Isomers with more than 2 chiral centers
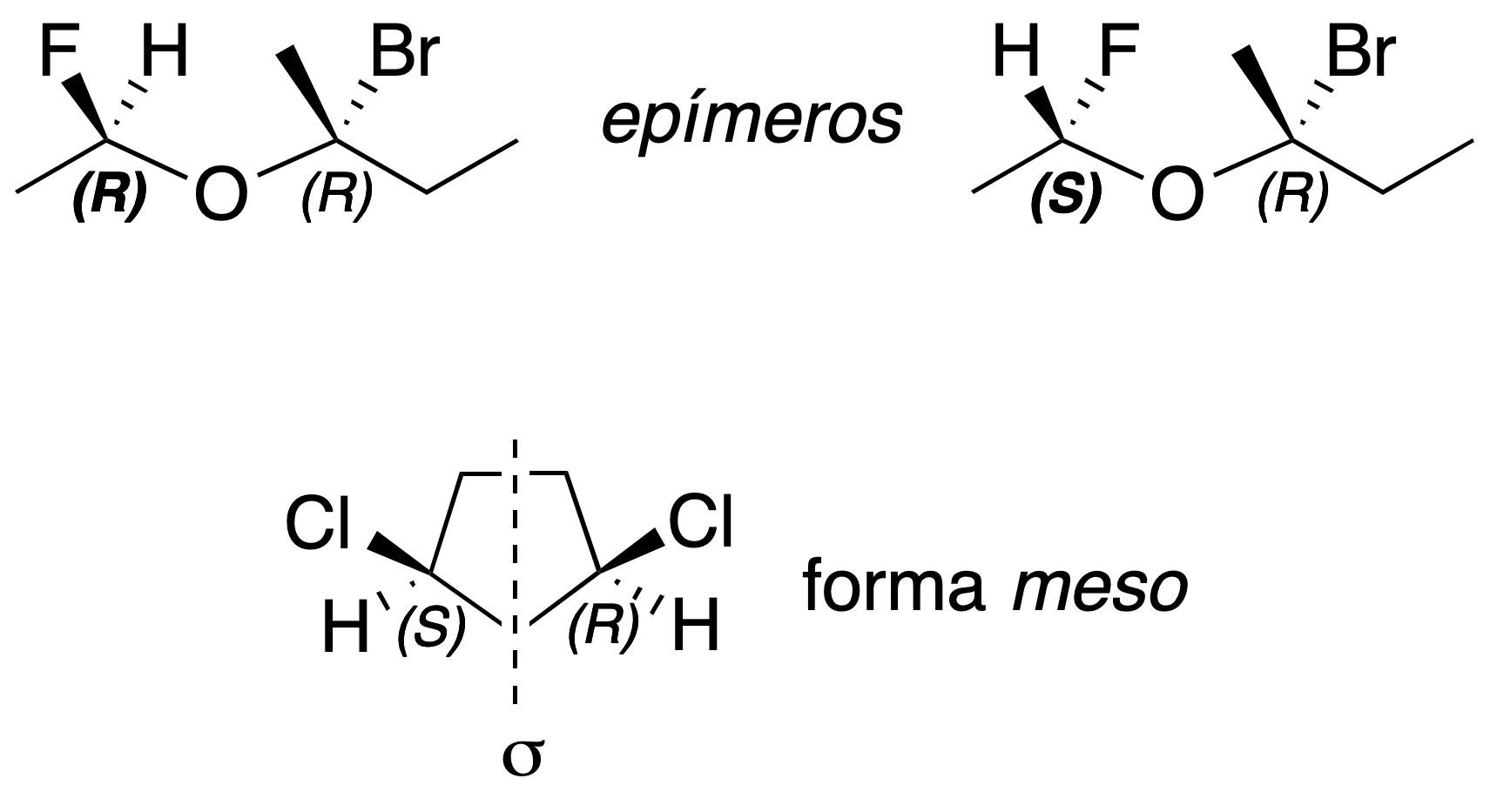
A molecule with n chiral carbons can present a maximum number of 2n stereoisomers, when it does not contain symmetry planes (Le Bel and Van’t Hoff).
If two diasteromers with 2 or more chiral centers differ only in the absolute configuration (see Cahn-Ingold-Prelogconvention) of a chiral carbon they are said to be epimers; and if a molecule has chiral centers but as a whole is achiral, due to the presence of a plane of symmetry, it is called meso form.
Cahn-Ingold-Prelog rules
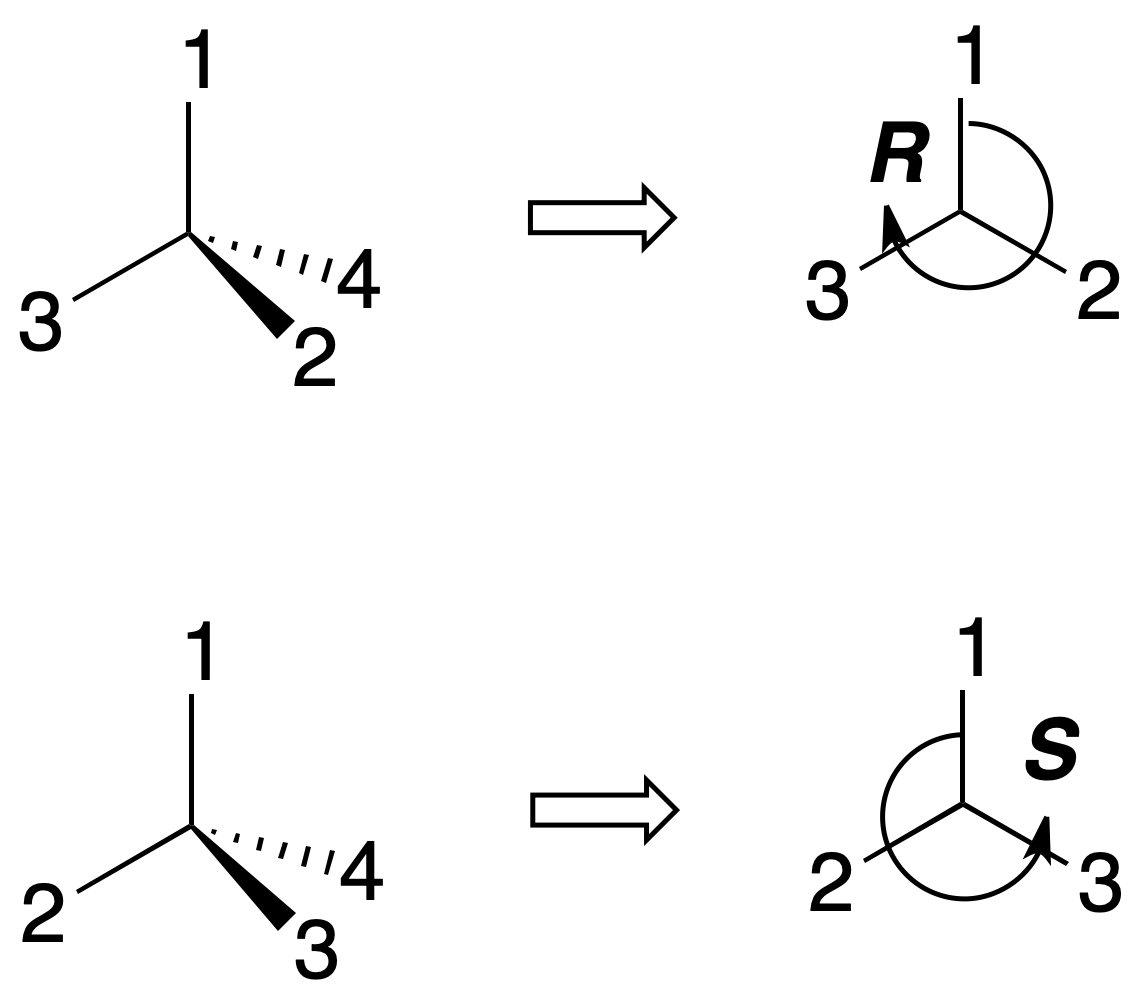
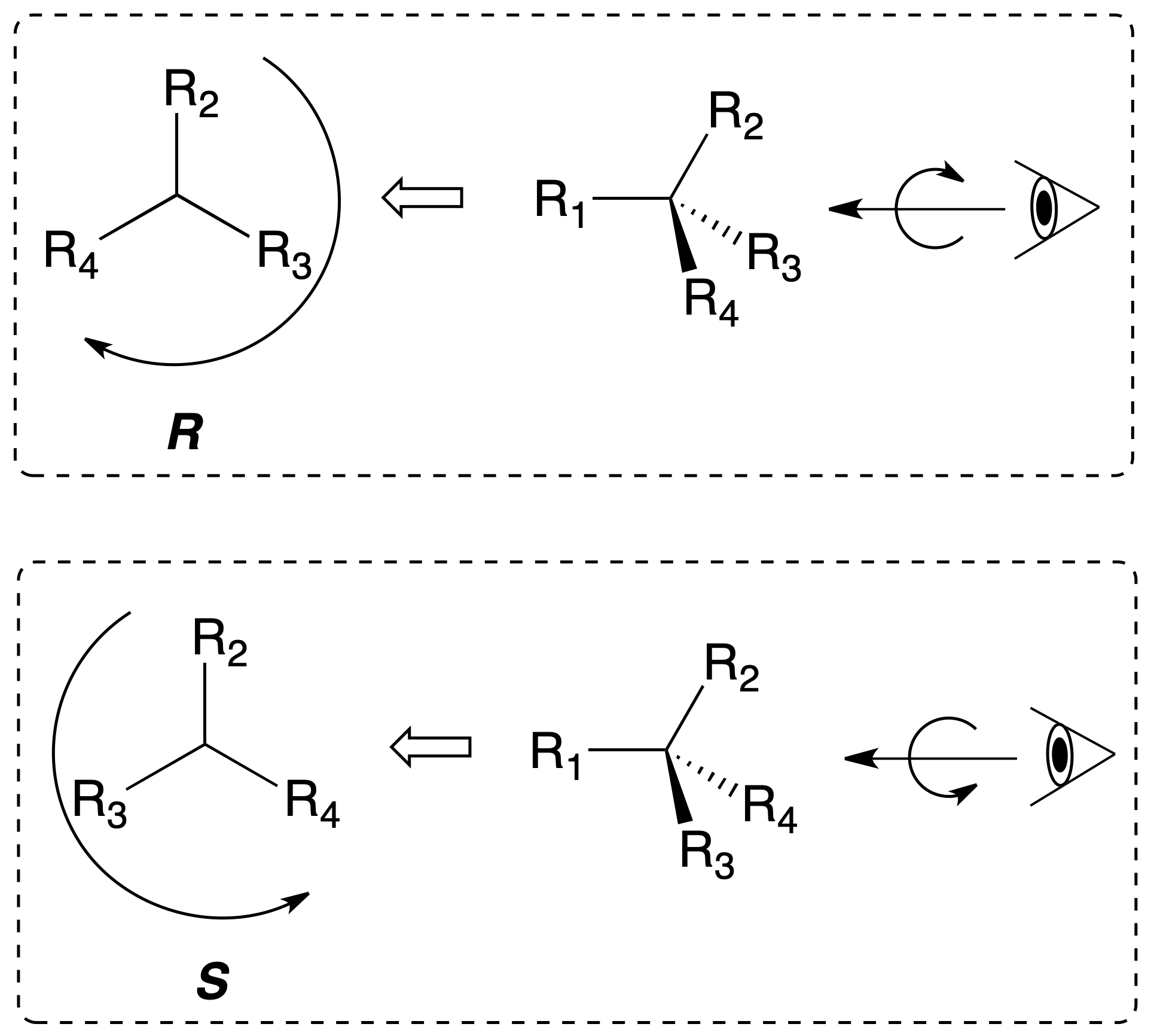
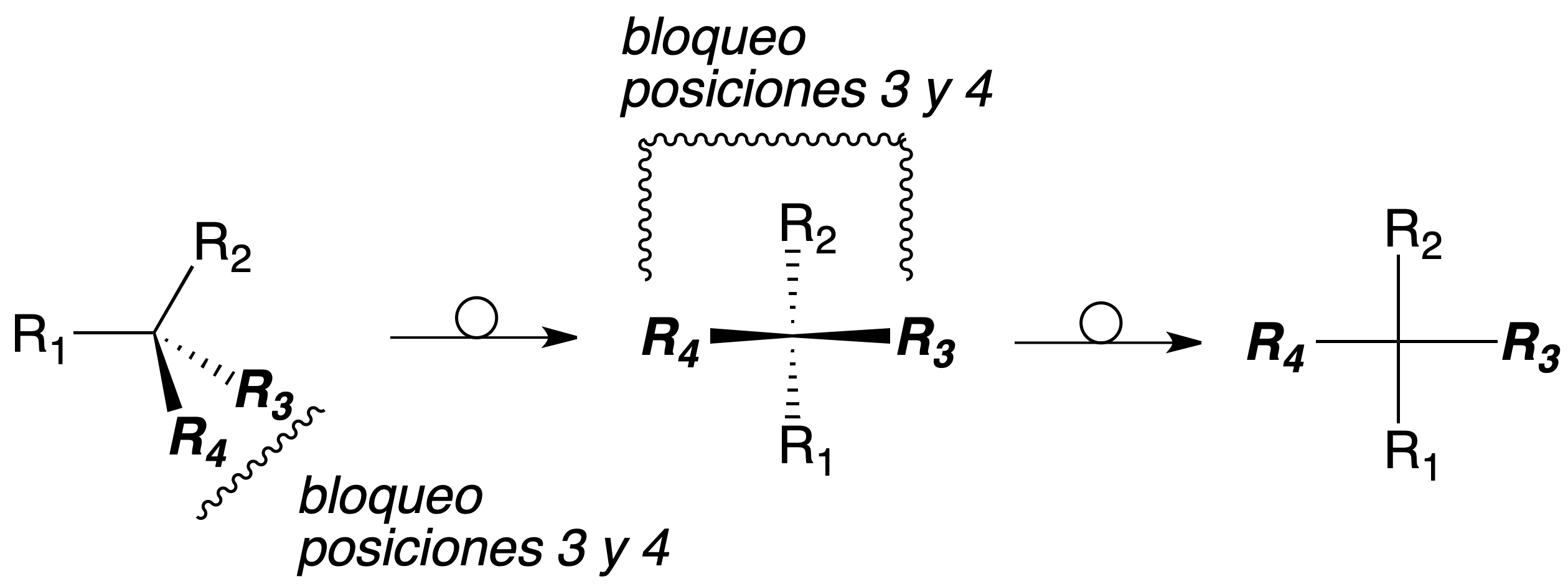
To establish the arrangement of the groups attached to a chiral carbon unambiguously, the concept of absolute configuration is defined. For this purpose, the substituents of the chiral center are ranked according to an order of priority. The carbon is rotated so that the lowest priority group (4) is towards the rear of the observer.
The carbon is assigned the R(rectus) configuration if these substituents are arranged in the clockwise direction from highest to lowest priority (1-2-3). Conversely, it is assigned the S (sinister) configuration if in the counterclockwise directionthey are arranged in order from highest to lowest priority (1-2-3), as shown in the figure:
To establish the priority of substituents on a chiral carbon, the following sequential rules are followed:
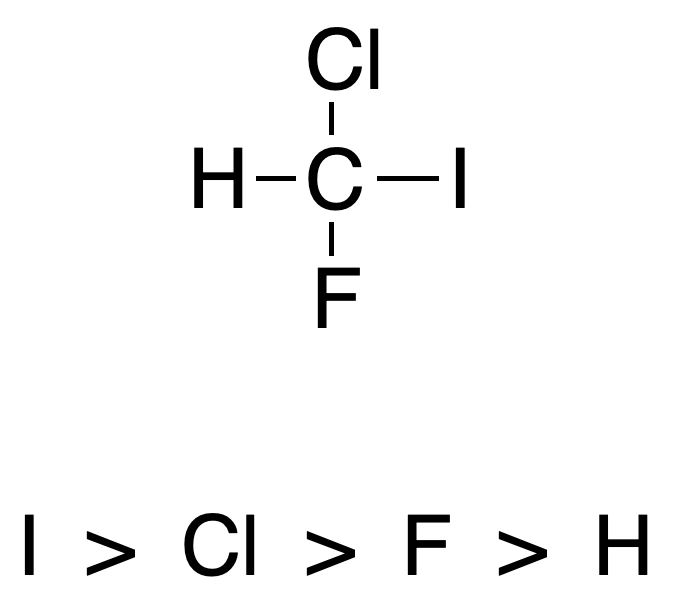
Rule #1
Atoms attached to a chiral carbon are classified according to their atomic number.
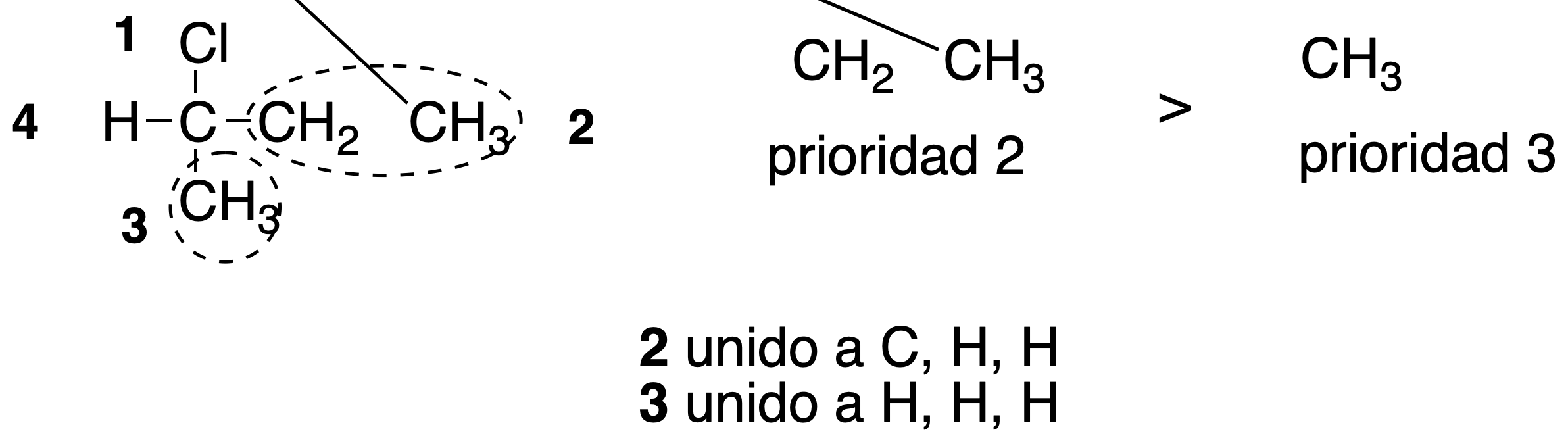
Rule #2
In the case where two atoms directly attached to the chiral carbon have the same atomic number, the atoms separated by two, three bonds, etc., with respect to the chiral carbon are considered until a difference is found.
Rule #3
If a branch is found along a chain without having established the priority, the chains of the groups with the highest priority of the bifurcation are compared and the difference is established on the basis of the atoms attached to these groups.
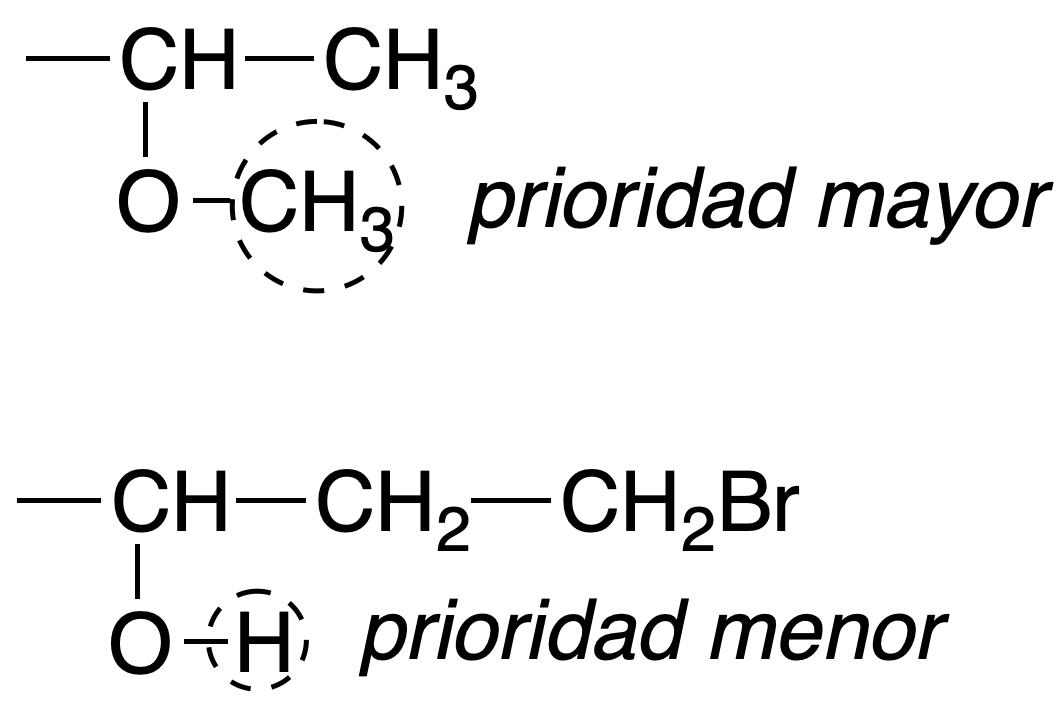
Rule #4
When there are multiple links, it is considered as if the links are saturated, as follows:
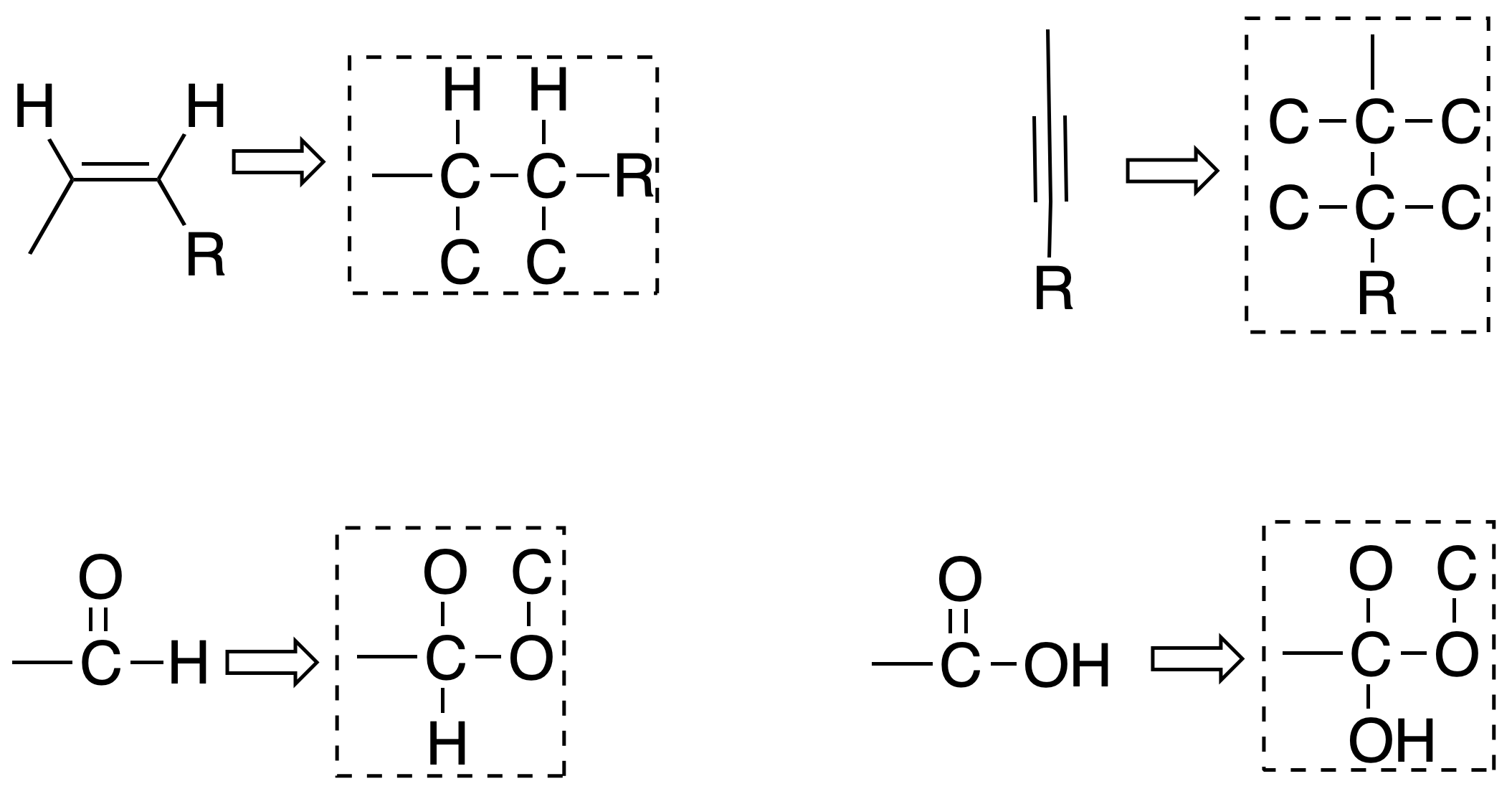
Rule #5
When two atoms are isotopes of each other, the one with the higher atomic mass has a higher priority. For example 14C > 13C.
Rule #7
If the difference between two substituents lies only in their absolute configuration, the R-configuration substituent has a higher priority than the S. Chiral carbons of this type are given the name pseudo-asymmetric carbons and are annotated with the lowercase letters r and s.
| Priority No. | Function |
| 1 | -I |
| 2 | -Br |
| 3 | -Cl |
| 4 | -SO2R |
| 5 | -SOR |
| 6 | -SH |
| 7 | -F |
| 8 | -OPh |
| 9 | -OCH2Ph |
| 10 | -OMe |
| 11 | -OH |
| 12 | -NO2 |
| 13 | -NO |
| 14 | -NMe2 |
| 15 | -NHEt |
| 16 | -NHMe |
| 17 | -NH3+ |
| 18 | -NH2 |
| 19 | -COOH |
| 20 | -COPh |
| 21 | -COCH3 |
| 22 | -CHO |
| 23 | -Ph-Me |
| 24 | -C≡CR |
| 25 | -Ph |
| 26 | -C≡CH |
| 27 | -CMe3 |
| 28 | -CH=CHMe |
| 29 | -C6H11 |
| 30 | -CH=CH2 |
| 31 | -CH2Ph |
| 32 | -CH2-C≡CH |
| 33 | -CH2-CH=CH2 |
| 34 | -CH2-CHMe2 |
| 35 | -CH2-CH2-CHMe2 |
| 36 | -CH2-CH2-CH2-CH2-CH3 |
| 37 | –n-But |
| 38 | –n-Prop |
| 39 | -Et |
| 40 | -Me |
| 41 | -H |
Criteria for the assignment of the double bond configuration
C=C double bonds can have different substituent orientations. When there are only two substituents (on C1 and C2) other than hydrogen, the two possible isomers can be distinguished by the notation cis / trans to indicate whether the two groups are located, respectively, on the same side of the double bond or on different sides.
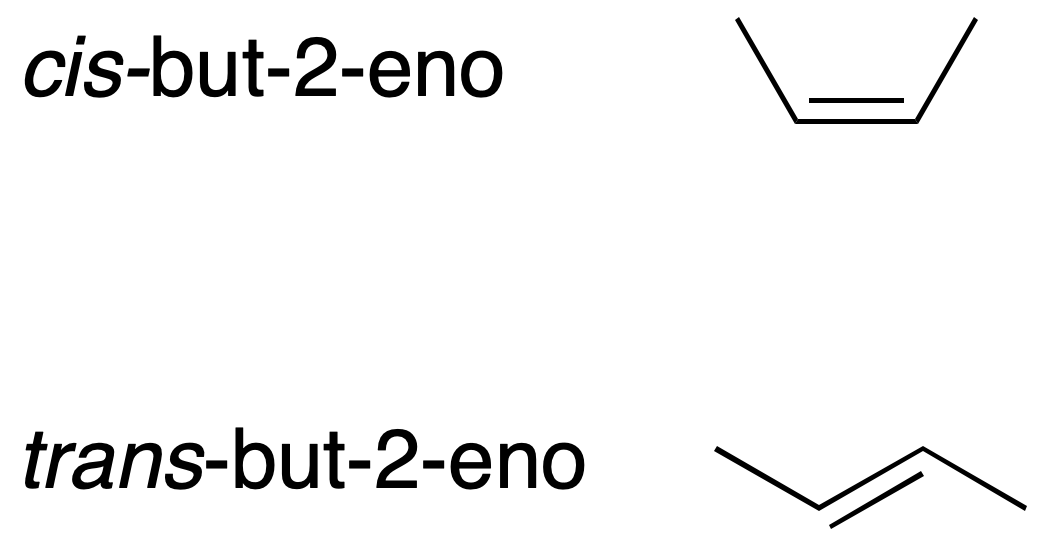
In more complex alkenes this way of differentiating the double bonds is not valid.

The nomenclature system adopted is based on the Cahn-Ingold-Prelog sequential priority rules seen above for the groups attached to each carbon.
If the higher priority substituents are on the same side of the double bond, the double bond is said to have a Zconfiguration and if they are on the opposite side of the double bond, the double bond is assigned the E configuration. The letter comes from the German term Zusammen and Entgegen.
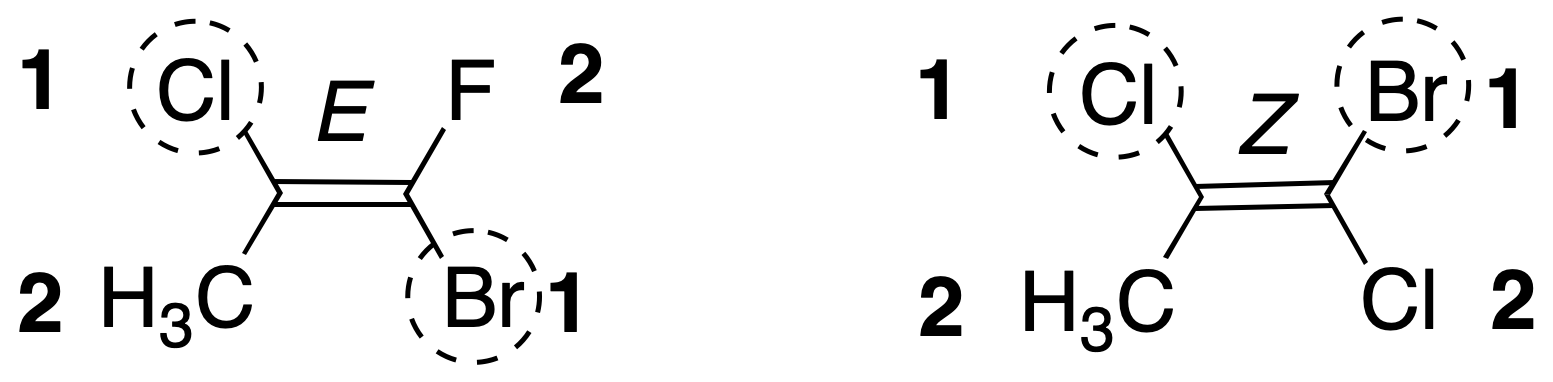
This system of nomenclature is more general than cis / trans, being fulfilled that the double bonds of configuration cis are Z and those of configuration trans are E.
Magnitudes related to optical isomerism
When we have a chiral product or a mixture of different chiral isomers there are a series of quantities that serve to indicate the purity of a sample:
Specific rotation [α]D25
Specific rotation is defined as the optical rotation angle (a) observed when a light beam of λ = 589 nm (sodium D line) passes through a sample in a 0.1 m cell with a 0.1 m pitch, 1 g/dL concentration (or 1 g/100 ml and 10 cm or 1 dm cell), and 25 ºC temperature.
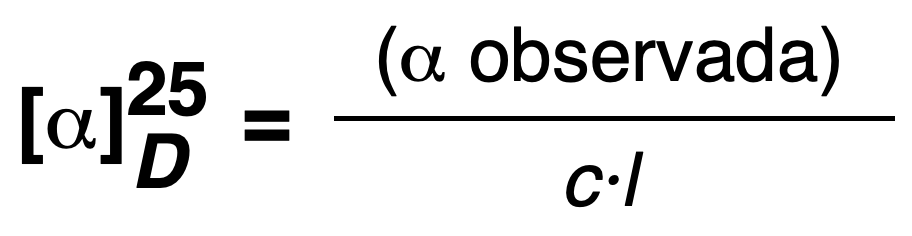
For two enantiomers this specific rotation has the same absolute value, but different sign.
Optical purity (o.p.)
The optical purity of a mixture is defined as the ratio of the observed rotation of the mixture divided by the optical rotation of the pure enantiomer.

Enantiomeric excess (e.e.)
The enantiomeric excess also expresses the relative proportion of (+) and (-) enantiomers in a mixture. The excess of the predominant enantiomer is calculated as a percentage of the mixture.
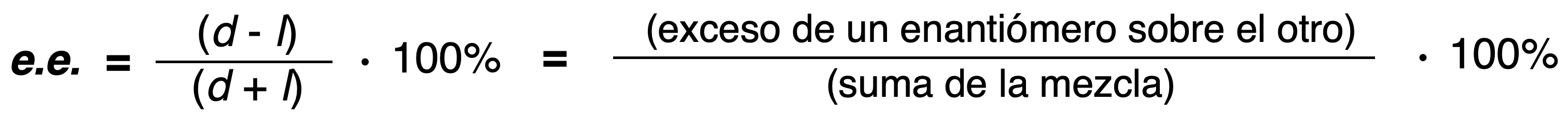
Relationship between organic structures
When asked what is the relationship between two organic structures we must answer the following questions successively shown in the following decision diagram:
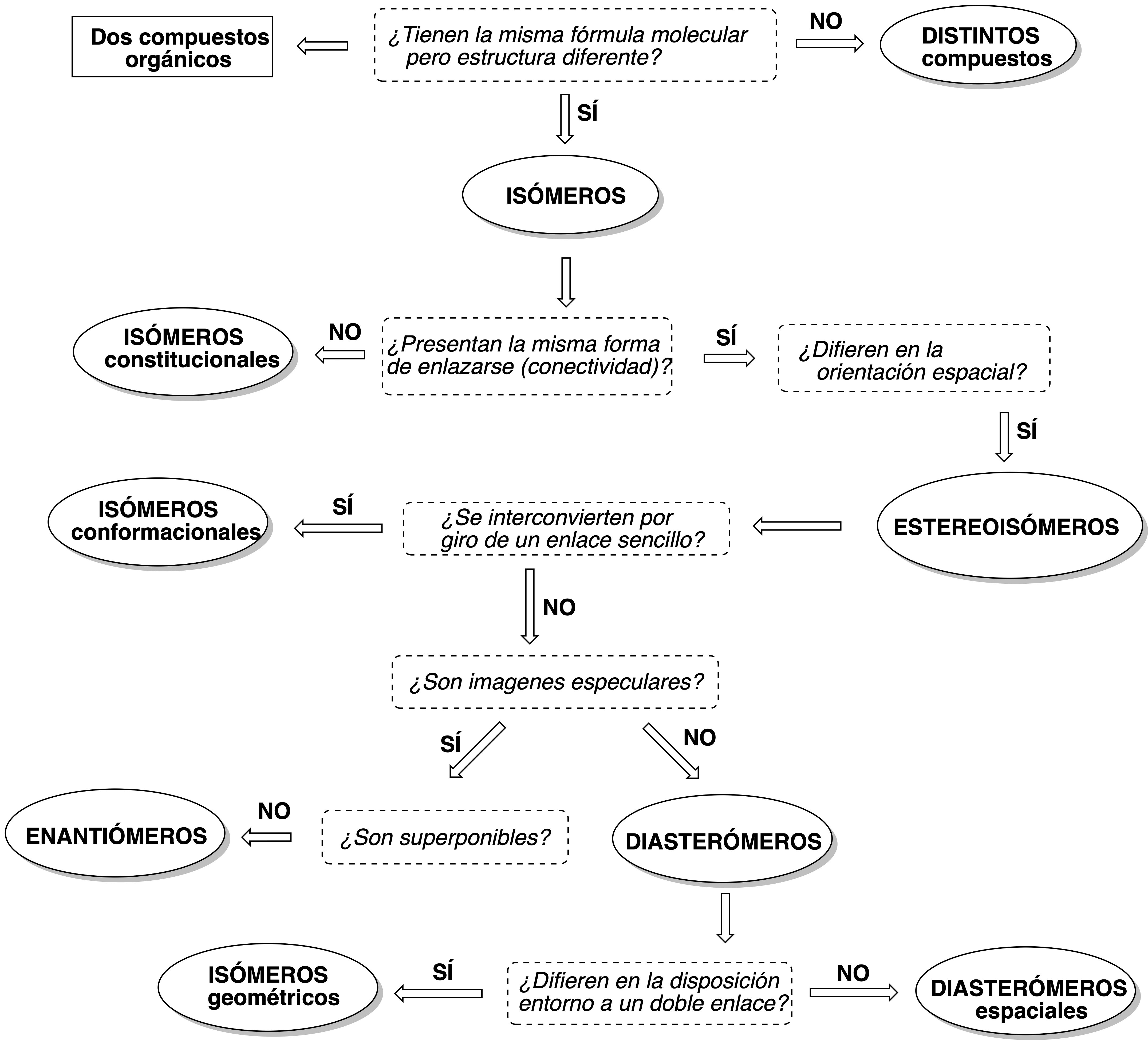
The following figure summarizes the different ways of representing molecules: sawhorse projection; Cram (wedges and dashes) representation; representation of cycles in the plane as regular polygons; Fischer, Haworth and Newmanprojections.
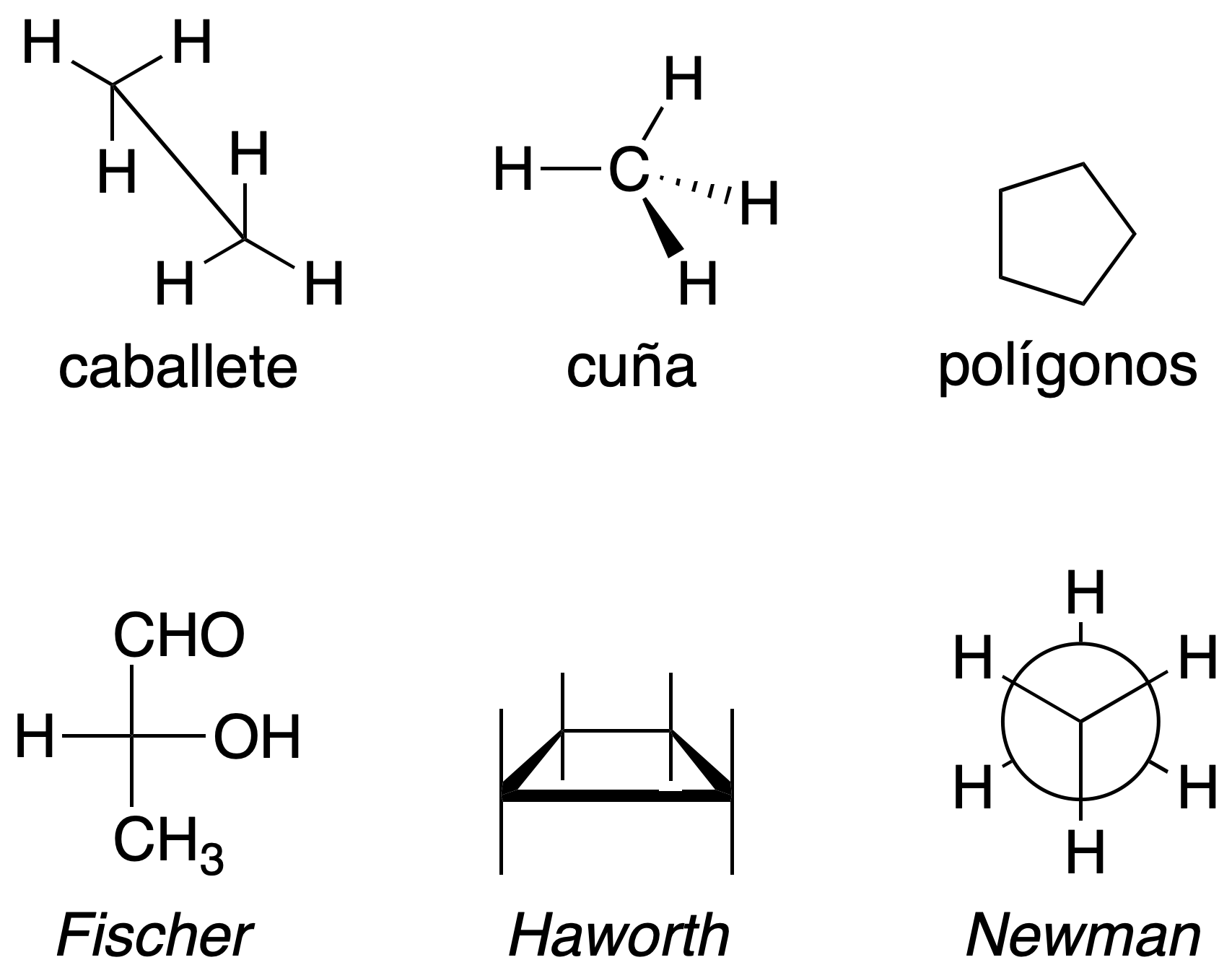
The same molecule can be represented in any of these ways and the analogy is not always evident; that is why we need to have the necessary vision for the interconversion between them. The easiest way to find the relationship between different stereoisomers is to determine the absolute configurations of all their chiral carbons and then compare the results obtained. In order to compare structures in different representations, it might be best to interconvert them all to the same representation.
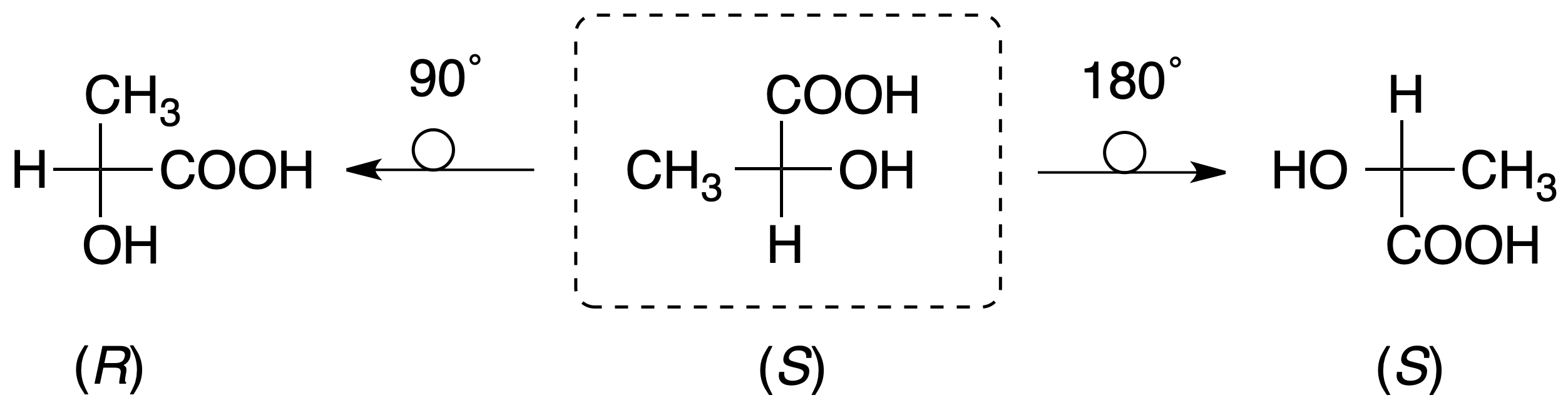
Still, it is not as simple as it seems; for example, the Fischer projection of one of the enantiomers of a molecule with a single chiral carbon ((R)-2-hydroxypropanoic acid or (R)-lactic acid) can be represented in 8 different ways:
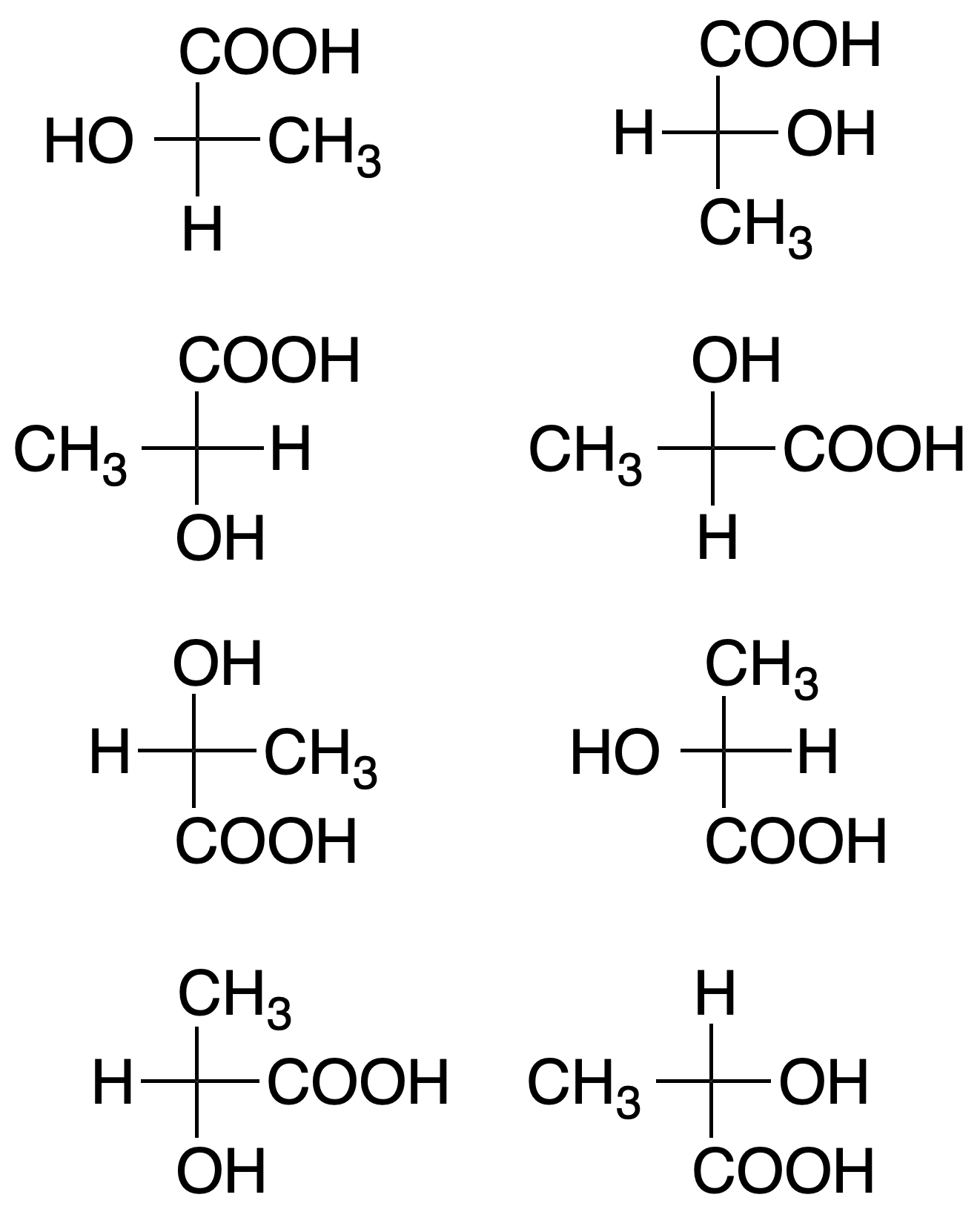
In such a projection, if two substituents are interchanged in position, the configuration of the chiral carbon changes. If an even number of permutations are made with two substituents, the configuration of the chiral carbon is maintained. However, if the number of permutations between two groups is odd, the configuration of the chiral carbon changes.

It should also be noted that in this representation the molecule can be rotated 180º about the plane that contains it, but not 90º because, in this case, the configuration would change:
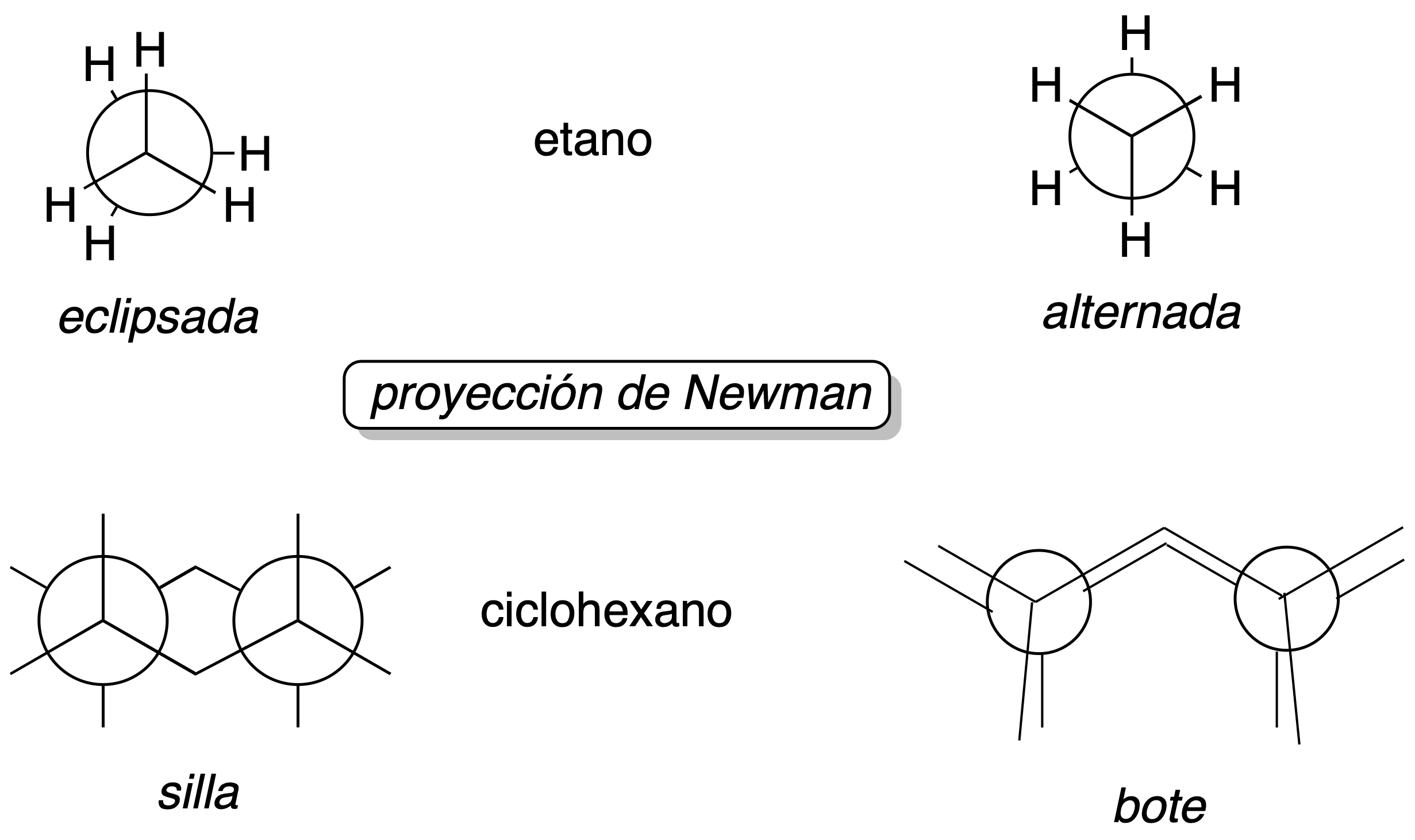
Conformational isomerism
We call conformers the different spatial arrangements that the atoms of a molecule can adopt as a result of the rotation of one or more single bonds in the molecule.
They are most easily visualised using the Newman projection.
Newman projection:
Example of how to obtain a conformation from another conformation
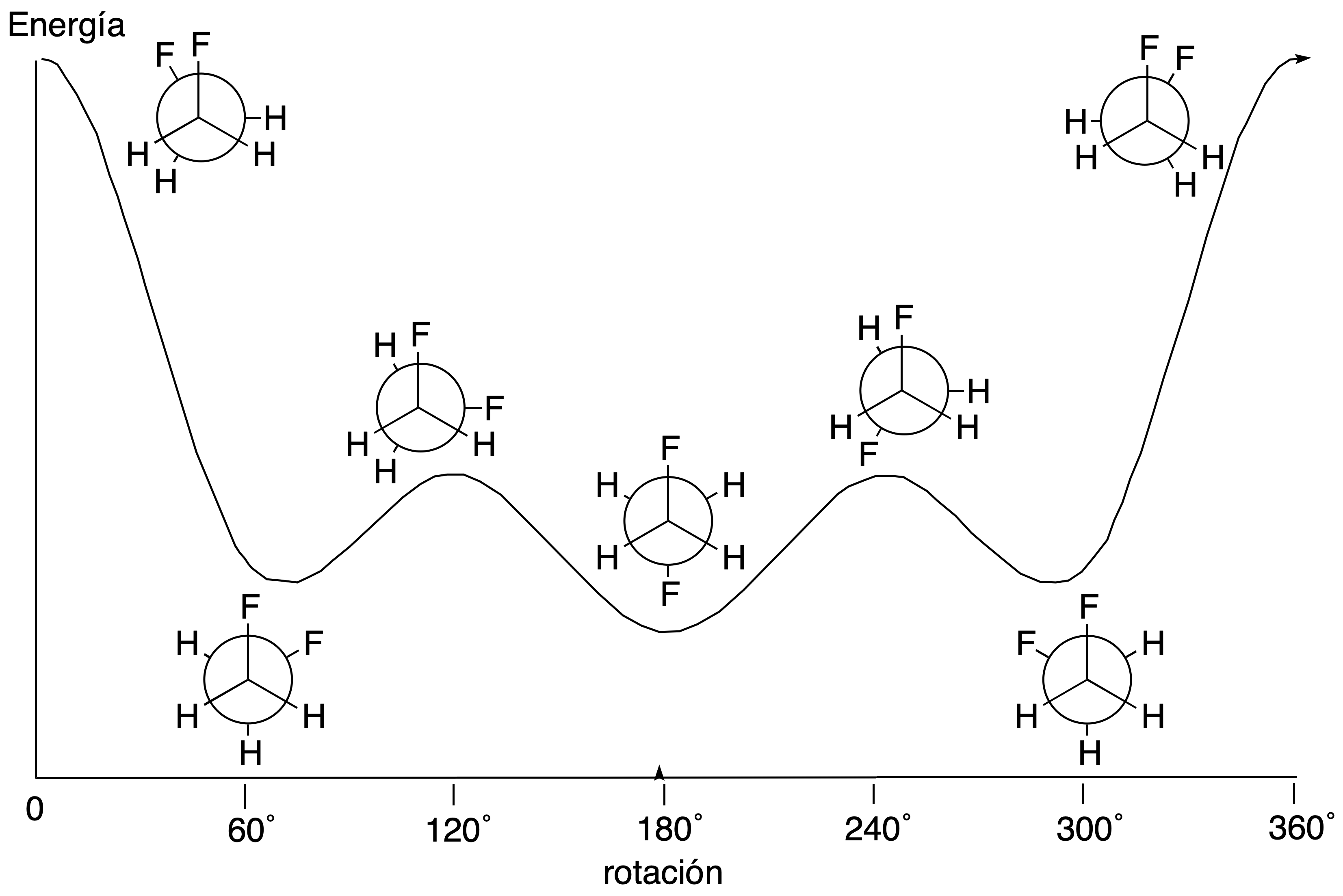
For example, the conformations of 1,2-difluoroethane will be obtained by starting from a given conformation and keeping one of the carbons fixed, rotating the other until obtaining an arrangement coinciding with the first one. If we start from the eclipsed conformation a, and we keep the carbon closest to the observer fixed, the farthest one is rotated in 60º steps.
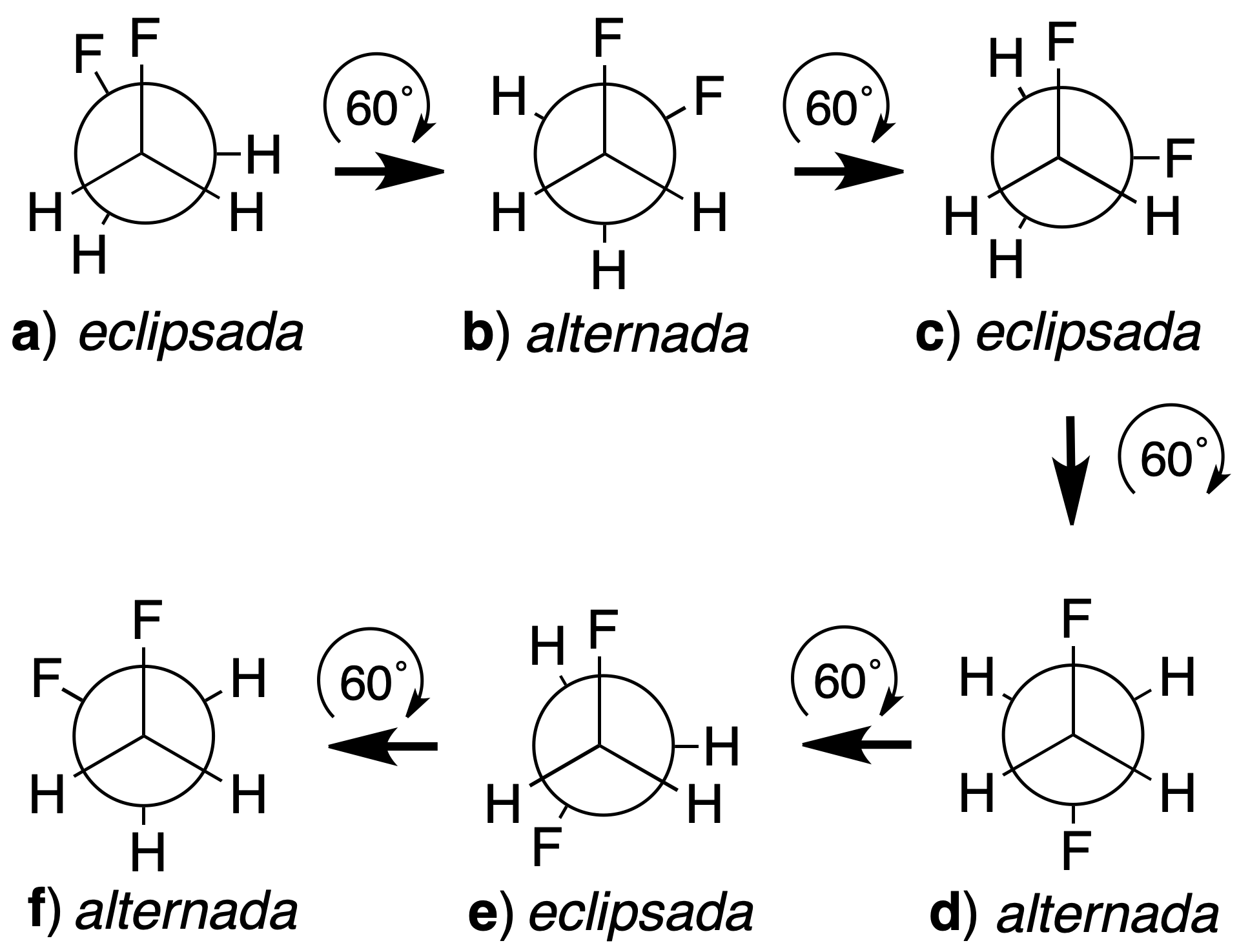
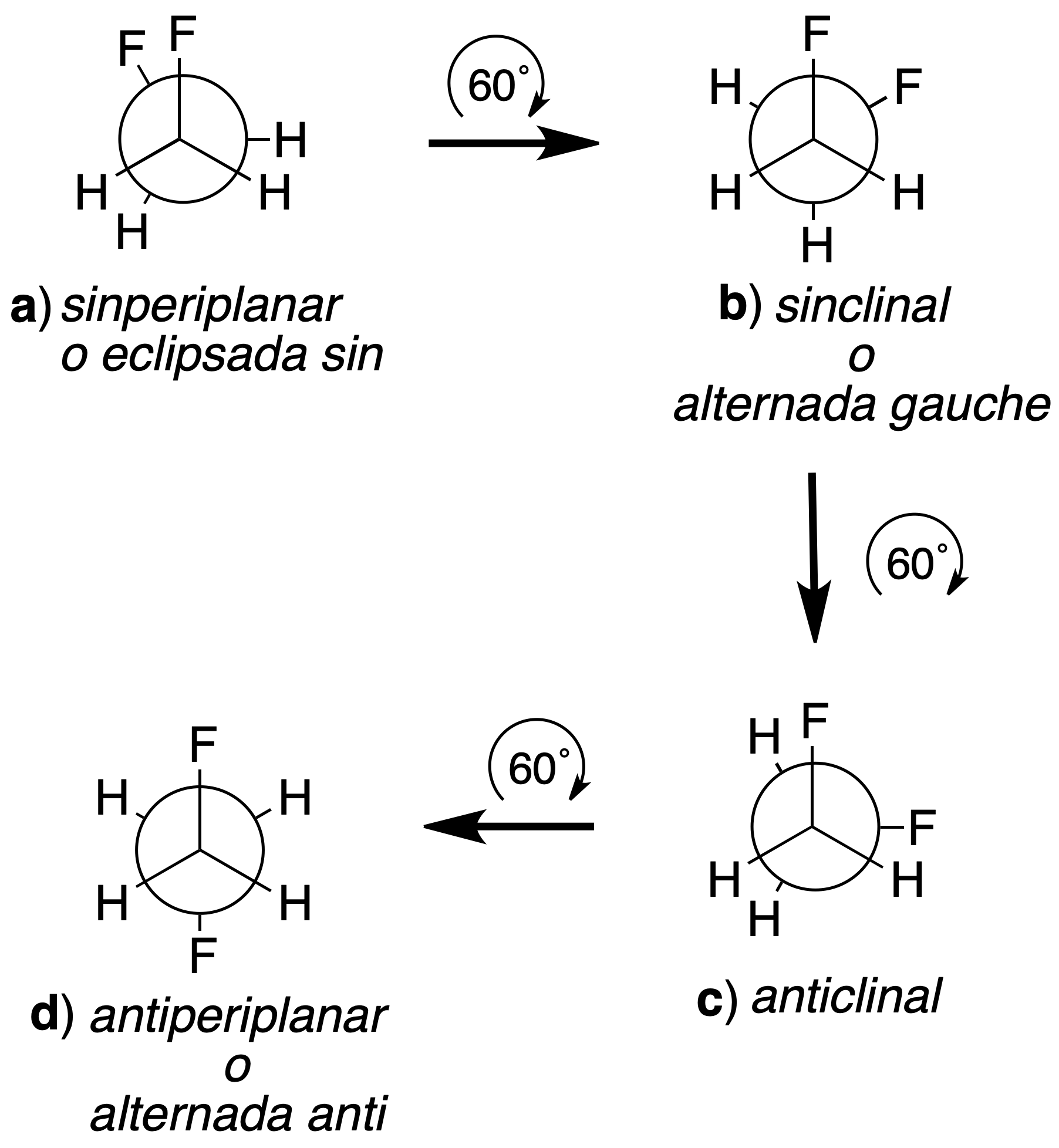
As a result, a–f conformations are obtained. The following criteria are used to name the conformations:
- When the bulky groups form dihedral angles of less than 90º, as occurs with the two fluorine atoms in the eclipsed a conformation, the prefix syn. is used.
- The prefix anti is used when the larger groups form dihedral angles greater than 90º, as occurs in the alternating dconformation.
- If the larger groups are located in different planes, as in b or in f, the clinal ending is used.
- We use the periplanar termination when the two most voluminous groups are located in the same plane (dihedral angle 0º) as in a or d..
Thus, the a, c and e conformations are eclipsed, while the b, d and f conformations are alternated. The e is equivalent to the c and the f conformation to the b. In the case of synclinal arrangements, the term gauche (French for twisted) is used as a synonym. According to these rules, conformations can be named as follows:
Example of how to obtain the preferred conformer
An additional issue in conformational analysis is to decide which is the preferred confomer of a given substance. Therefore, since all conformers are interconvertible with each other by single bond twist, all conformers will be present at equilibrium. As a consequence, their relative abundance will depend on their relative stabilities. Thus, to determine which is the most stable, it will be the one with the least steric and polar interactions.
Cyclic compounds (especially cyclohexanes) will be analyzed in a similar way, although, in this case, the most important interactions are the 1,3-diaxial ones (since there are no eclipsed conformations). These are usually quantified in energetic terms and even allow us to calculate the distribution of confomers at equilibrium.