Written by J.A Dobado | Last Updated on April 22, 2024
It is the most rigorous method for determining whether a pericyclic reaction is allowed or not, and it was developed by Woodward-Hoffmann.
In a reaction, if there is an element of symmetry that is conserved along the entire reaction coordinate, it must be possible to correlate the orbitals of the reactants with the orbitals of the products, so that this correlation will be given by conserving the symmetry of the element that is conserved along the reaction coordinate. When this correlation correlates bonding orbitals in the reactants with bonding orbitals in the products, the reaction will be allowed by symmetry, but when this correlation establishes between bonding and anti-bonding orbitals, then the reaction will be forbidden by symmetry. This is so because in the bonding and anti-bonding levels there is a very large energy difference, in order to pass from a bonding level to an anti-bonding one a very large energy barrier must be passed, and therefore if two orbitals that are both bonding are correlated, that correlation occurs without an energy barrier, and therefore if two orbitals that are both bonding are correlated, that correlation occurs without an energy barrier, if the correlation is established between bonding and anti-bonding orbitals, it has to occur with a significant energy barrier, therefore the former will be allowed by symmetry while the latter will be prohibited.
In order to make the correlation diagrams the first thing to study is the diagrams involved in the reaction, both in the reactants and in the products, and once we have located the orbitals, we have to look for the symmetry element or elements that are conserved along the entire reaction coordinate. Once we have these symmetry elements, we proceed to classify the orbitals of the reactants and products with respect to those symmetry elements. Then, the orbitals in the reactants have to be transformed into those of the products conserving the symmetry.
Let us suppose the electrocyclic reaction of butadiene to cyclobutene. In this reaction we have the orbitals that interact in the reactants which are those of the butadiene system which are the only ones involved, in the products we have the p system of 2 electrons and the s system also of two electrons that are formed throughout the reaction. Normally, to establish the correlation diagrams it is necessary to represent the orbitals ordered by energy. Of the orbitals of the products the one with the lowest energy will be the bonding s and the one with the highest energy will be the s* and the one with the highest energy will be the s* and in the middle we will have the two p orbitals.

Now we have to consider the reaction. This reaction can be produced through an electrocyclic mechanism with two possible alternatives, one conrotatory and the other disrotatory, and what we have to do is to predict with which stereochemistry this reaction will occur. To do this we must recognize the symmetry elements in such a way that they are conserved along the entire reaction coordinate. For this we will look at the cyclobutane system. For which we assume an a substituent in cis upward arrangement. To analyze the element that is conserved, we start from the reactants and see how the reaction evolves. Assume a conrotatory electrocyclic reaction at a slightly later stage both will have rotated a little in the same direction, so that at the end one of the substituents will be inward and one outward. The only element of symmetry that is conserved throughout the reaction is a C2 axis. Since the plane of symmetry is no longer conserved as soon as the reaction begins.
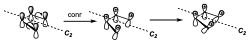
One of the considerations to take into account is that the interacting orbitals along the reaction coordinate are reduced to maximum symmetry, i.e. if there are substituents they are eliminated.
Once we have located the symmetry element that is conserved throughout the reaction, the different orbitals are classified into S (symmetric) or A (antisymmetric). The first one is antisymmetric, since if we turn 180º the + signs are downwards. Now, we can see which of the different levels are occupied and which are not. When we study the energy resulting from these OM, the last bonding orbitals have very similar energies and all negative, while the first anti-bonding orbital has a very different energy from the last bonding orbital and also positive (although it is not represented in the drawing).
Now we have to perform the correlation between orbitals, a given orbital as it evolves has to correlate in the products with an orbital of the same symmetry. So we see that the two bonding levels correlate along the reaction coordinate with the two anti-bonding ones. Therefore this correlation that is established along the reaction coordinate occurs without a significant energy barrier and therefore the reaction will be allowed by symmetry.

Let us suppose now the disrotatory reaction. In this case the conserved symmetry element is the plane.
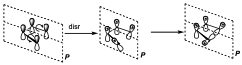
Now the correlation can be established as indicated above. Now the correlation diagram is different. We see that the second bonding orbital in the reactants correlates with the first anti-bonding orbital in the products, therefore along the reaction coordinate it would place two electrons in an anti-bonding level, and in order to do that it has to overcome an important energy barrier, therefore the reaction will be forbidden by symmetry.
So let’s make some considerations in order to make correlation diagrams.
- The first thing to do is to locate the orbitals involved in the reaction, in the reactants and products. Then we have to consider the symmetry elements of the system that are conserved along the reaction coordinate. These symmetry elements must be sought in such a way that they bisect the bonds that form or break along the reaction coordinate (this is the general rule for locating these symmetry elements).
- Once these symmetry elements are located, the orbitals of the reactants and products are classified with respect to these symmetry elements.
- Then the orbitals of the products and reactants are correlated in such a way that they maintain symmetry along the reaction coordinate. So when drawing the correlation lines it must be taken into account that correlation lines joining orbitals of the same symmetry cannot cross.
- The orbitals involved must be reduced to their maximum symmetry; if there are substituents that are not involved in the reaction, they are eliminated to take into account the symmetry of the interacting orbitals.
- When the correlation is between orbitals of the same type, i.e., bonding orbitals in the reactants that correlate with bonding orbitals in the products, etc. the reaction takes place without an energy barrier and will therefore be allowed. When this is not fulfilled, the reaction is symmetrically forbidden. In the fundamental state a reaction will be symmetrically allowed only when all electron pairs in bonding orbitals in the reactants are transferred by a correlation to bonding orbitals in the products without an energy barrier.
With respect to point 3, let us suppose that we try to perform a correlation of this type:

This correlation does not occur, because the line that joins two symmetrical orbitals with the other that joins two other symmetrical orbitals crosses. This is a representation of the reaction coordinate where it is seen how these orbitals are correlated. As the reaction progresses those orbitals of the reactants that are symmetrical come closer in energy so that there comes a time when they have very similar energies, and they are two orbitals that have the same symmetry and one is occupied and one is unoccupied, then by approaching in energy they could interact with each other so that they produce two orbitals with different energies again, and so on, then the process can not be carried out by this interaction between orbitals of the same molecule.
As we have seen in the excited state things change, so that what is forbidden in the ground state will now be allowed. Let’s see how the correlation diagrams explain this fact perfectly.
If we put the correlation diagram back to the ground state for the disrotatory case, we see that there is a double energy barrier so that the reaction cannot go well in either the forward or reverse direction.

If we now put the same scheme with the same symmetry where one of the electrons has passed to an excited level, that is, we are representing the first excited state.

It must be considered that the triplet states will not give rise to pericyclic reactions since they are biradical and therefore will act through radical reactions. Now the correlation is established the same as before, but in such a way that the first excited state of the reactants correlates with the first excited state of the products and therefore if there is an increase of energy to take the electron to a higher energy level, in the other step there is a release of the same amount of energy. And therefore this reaction goes from being forbidden to being allowed, i.e. the electrocyclic reaction with four disrotatory electrons is allowed in the excited state.
Let us now look at examples of cycloaddition reactions. The simplest example of p2s+p2s cycloaddition reactions to give rise to cyclobutane. In the supra–supra topology the two ethylene molecules approach each other in parallel so that the interaction between the orbitals is established, so in that reaction there are two symmetry elements that are conserved throughout the reaction. We have the plane that is at the midpoint of the two ethylene molecules. And the other one is the plane perpendicular to that.
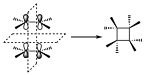
Once we have the elements, let’s look at the orbitals involved in the reaction, both in the reactants and in the products. On the one hand we have the two two-electron p-systems and on the other hand the two two-electron s-orbitals of the cyclobutane system. The p1 and p2 orbitals with respect to the P1 plane and with respect to the P2 may not have the correct symmetry. If we look they are symmetric for P2 but with respect to P1 the p1 orbital becomes p2(antisymmetric). The same will happen with the s orbitals that have been formed, they will have correct symmetry with respect to P1but not with respect to P2, where one transforms into the other, therefore a linear combination of both will have to be made so that they again have the correct symmetry.
Then, with respect to p1 we have the bonding orbital and the anti-bonding orbital, with respect to p2 we have again the bonding orbital and the anti-bonding orbital. Therefore, we have to generate orbitals of correct symmetry from those that do not have it, there will be interactions between the orbitals that have similar energies, on the one hand we will have the interaction of the linker with the linker and on the other hand the interaction of the anti-linker with the anti-linker. As they are orbitals of the same symmetry two new orbitals will be generated, the process does not lower energy since the orbitals obtained are made from occupied orbitals, but this generates orbitals that have correct symmetry. So the orbital ys = p1e + p 2e will be the bonding contribution of both.
yd = p1e – p 2e . The same can be said with respect to antibonds: ys* = p1a* + p2a*; yd* = p1a* – p2a*

We are interested in knowing what shape these orbitals will have in order to classify them with respect to the symmetry elements. ys will be the bonding contribution of both orbitals p1 and p2.
It is a bonding type orbital since it places net density between the new bonds being established and also places net density between the previously bonded carbon atoms.
With respect to yd.
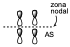
It will be an anti-bonding contribution of the bonding orbital of p1 with the bonding orbital of p2 since in the zone of formation of the new bonds there is a node, but it is a bonding orbital since in the zone where the two carbon atoms are located there is a net electron density and therefore it is a bonding orbital even though it is an anti-bonding contribution to the new bond.
Both orbitals are occupied.
With respect to ys.
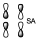
It is a bonding contribution of both but both are anti-bonding, therefore as a whole the orbital will be anti-bonding. We must consider that these two osrbitals are approaching, but they are far apart, and in the middle zone there is a null contribution to the bond, therefore it is an anti-bonding orbital. But it is the bonding contribution of two anti-bonding orbitals. This implies an orbital that is favored in energy with respect to the previous ones but it is still an anti-crossing orbital.
Lastly, we have yd*
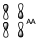
Which will be an anti-bonding contribution from two anti-bonding orbitals.
These two levels are unoccupied.
Then we have to make the same considerations with respect to the σ orbitals that are formed, so that the combination of these orbitals will give rise to 4 new orbitals of correct symmetry (σs, σd, σs*, σd*) that will have the following form:
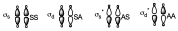
We have put it in the same way but obviously the shape of the anti-bonding orbitals is different from that of the bonding orbitals.
Once we have the orbitals and in the products with correct symmetry, we have to classify them with respect to the elements of symmetry P1 and P2, in such a way that the first symbol is with respect to P1 and the second with respect to P2. Thus we will have:

Therefore the correlation must be done as indicated there, where we see that the yd orbitals in the reactants correlate with the σs* orbital in the products, so that two electrons of bonding levels, which means that this reaction must have a very important energy barrier imposed by the symmetry and the reaction will be forbidden.
Let’s now look at Diels-Alder’s reaction.
It is a π2s+π4s reaction, in this case there is only one symmetry element that is conserved throughout the reaction, which is the P1 which is a vertical plane perpendicular to the plane of the paper.
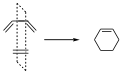
With respect to this plane, both components of the reactants, the two-electron p orbital and the four-electron p orbital have correct symmetry. The orbitals of the reactants and of the products will be:

All these orbitals have correct symmetry, with respect to this plane any point of an orbital is transformed into another of the same orbital, it may or may not change sign and consequently be symmetric or antisymmetric.
In the products we have two s bonds formed by interaction of p orbitals of the reactants, and we see that the orbitals of those bonds by themselves do not have correct symmetry with respect to the plane therefore they must interact to give 4 orbitals of correct symmetry, since the two are equivalent one transforms into the other. By the interaction of the two bonding orbitals de two bonding s orbitals must be formed, one with a bonding contribution and the other with an anti-bonding contribution. On the other hand by the interaction of the two anti-bonding orbitals, two anti-bonding s orbitals have to be formed, one with a bonding contribution and one with an anti-bonding contribution.
In principle we can think that the correlation is very simple and in the way the three linking levels are transformed into linking levels in the products
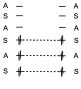
This can be so and the reaction will be allowed by symmetry, what happens is that the correlation of orbitals is not the one we have put there, since the lowest energy orbital of the reactants is not transformed into the lowest energy s orbital of the products, but that orbital must actually be transformed by interaction with the p system in the third, because when interacting with the p system of two electrons these two ends are canceled and the only thing that would remain would be the p orbital of two electrons in the middle. And from the third of the reactants with the first of the products since that p orbital when interacting with the p orbital of 4 electrons must form the two s orbitals. That should be the correlation and not the previous one, what happens is that there is a crossing between lines of the same symmetry, that is impossible and then what there is is an attempt of correlation of this type.

That is, the third one tries to correlate with the first one of the products, but as the interaction with the other correlation line occurs, it ends up correlating with the third one. This explains the small energy barrier that exists in the Diels-Alder reactions. In both ways the correlation is established between binding levels of the reactants and binding levels in the products and therefore the reaction will be allowed by symmetry.
With respect to the correlations in antarafacial cycloadditions, p2s+ p2a, an interaction had to occur as depicted in the diagram:

The element of symmetry that is conserved is the C2 axis, which bisects both systems, so that now the orbitals involved in the reactants and in the products, are the two p orbitals in the reactants, two bonding and two anti-bonding, both have correct symmetry with respect to the C2 axis. With respect to the products we have the two s orbitals that are formed that do not have correct symmetry with respect to the C2 axis since one transforms into the other but not into themselves, but the interaction between both can be established since they are equivalent to give 4 orbitals of correct symmetry.

With respect to the symmetry element, those 4 s orbitals are already symmetric. So you can establish the interaction as we have there represented, and then we see how a 4-electron supra–antara interaction involving an anti-Hückel ring is allowed by symmetry since it correlates the two bonding levels in the reactants with the two bonding levels in the products and the same for the anti-bonding ones.
After we looked at the correlation diagrams and the interaction diagrams to try to describe when a pericyclic reaction will occur or not and especially what stereochemistry it will have when it occurs. If you look at the interaction diagrams we built them from the orbitals that we then used in the correlation diagrams and what we did when we built the interaction diagrams was to take those orbitals and look at the topology of the reaction to try to predict whether those interaction diagrams were aromatic or antiaromatic, seeing especially in the topology of the reaction whether there was supra or antara topology which was what fundamentally caused the Hückel or anti-Hückel type rings and therefore the aromatic or antiaromatic character.
All this led Woodward and Hoffmann to think that valuable information could be extracted from the interaction diagrams, since they were constructed from the orbitals that were then used in the correlation diagrams, and then possibly information could be extracted with respect to those interaction diagrams, but considering instead of the orbitals involved in the reaction as such, to consider components of the interaction diagram.
Suppose for example an electrocyclic reaction, when constructing the interaction diagram we considered the p and sorbital in such a way that we considered the interaction diagram considering the interaction that was inside each orbital before the interaction occurs and after it occurs between the intervening orbitals, so that we said that it was suprafacial when those orbitals intervened by extremes with the same sign, while it was antarafacial when they did it with orbitals of different sign. The disrotatory opening caused a supra–supra interaction.
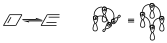
So that is the interaction diagram. The conrotatory opening implies that one of the components acts in a suprafacial way which causes an interaction diagram with a different topology.
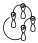
It does not matter which interaction diagram we have, since we can divide it into components, so that a component of an interaction diagram is defined as parts of the interaction diagram that connect lobes of the same sign and also have an even number of electrons, which can be the orbitals involved in the reaction or can be part of those orbitals. Also if we look at the interaction diagram for the electrocyclic opening or closing reaction of a system with 6 electrons, for the disrotatory opening it would be:
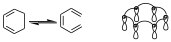
If we put the signs it is a diagram in which all the lobes of the same sign are joined, and we see that on that diagram we can define different components, so we can have one component of two and another of four, but we can also have 3 components of 2. That is a Hückel ring with 6 electrons, and therefore aromatic, and it is allowed.
If we study in this way many reactions by constructing their interaction diagrams and divide them into components and take into account whether they act supra- or antarafacially and the number of electrons, conclusions can be drawn which are those that Woodward and Hoffmann will draw to establish what they called the generalized rules, which are empirical rules that allow us to say when a pericyclic reaction is allowed or not in a rapid way. These rules are:
A pericyclic reaction is thermally allowed if the total number of 4n+2 electron components acting suprafacially plus the number of components with 4n electrons acting antarafacially is odd.
This rule can be further simplified, since all components can be reduced to two-electron components, then the rule can be changed to: a reaction will be thermally allowed when the number of two-electron components acting suprafacially is odd.
In the previous case for example we have 3 two-electron components and all suprafacially, therefore the reaction is allowed. However the first one which is an interaction diagram with two suprafacial components the reaction will be forbidden. If one of the components acts antarfacially then we are left with only one suprafacial component and the reaction is allowed.