What are pericyclic reactions?
Pericyclic reactions are concerted reactions in a single step (therefore they are not radical reactions involving several steps), and as the name indicates, they occur in a process in which the transition state presents a closed loop of interacting electrons, so that the shape of this loop implies special characteristics of the different reactions, causing some reactions to occur and others not, This implies that they are stereospecific (only one of the possible stereoisomers is obtained), therefore in the experimental study it is sought that the reactions are stereospecific, if it is found that there is a certain racemization, etc., a pericyclic mechanism can be totally ruled out. The fact that they take place in a single step implies that there are no reaction intermediates that can be studied, which is a problem for their experimental study.
We are going to develop Woodward and Hoffmann’s theory from several points of view. First we will approach the theoretical aspects where we will try to predict when a given reaction occurs and with which stereochemistry. In a second step we will try to demonstrate experimentally if pericyclic reactions of the different forms introduced by Woodward-Hoffmann exist or not.
These definitions are:
- Cycloaddition reactions: from two separate systems a single cyclic system is formed.
- Electrocyclic reactions: within the same system a cyclic system is formed.
- Sigmatropic transpositions: a group transposes along a π-system of electrons.
- Chelotropic reactions: these are cycloaddition reactions in which one of the components is a single atom.
- Group transfer reactions.
They are reactions in which all the bonds are formed and broken to the same extent along the reaction coordinate, this always occurs, in a concerted reaction, one bond may always be more formed than the other broken in the transition state, i.e. the transition states need not be symmetrical or in other words the reaction need not be synchronous. The fact that it is concerted does mean that it occurs in a single step and the bonds are broken and formed simultaneously but not synchronously, therefore in the transition state the bonds that are formed may be more formed than broken those that are broken. This is always the case, so in SN2 the nucleophile may be more attached to the carbon undergoing substitution than the bond of the broken leaving group.
The definitions made for the different types of pericyclic reactions are somewhat arbitrary, because all pericyclic reactions can be considered as a particular case of cycloadditions. But let us first define the fundamental characteristics of these different pericyclic reactions, their stereochemistry, etc., and then we will see how those which are not cycloaddition reactions can be studied as particular cases of cycloaddition reactions.
Theoretical models for the study of pericyclic reactions
There are several alternatives for carrying out a theoretical study of this type. Thus we have the pioneering work of Woodward-Hoffmann, from which many others were derived and which we will deal with last. First we will look at a more qualitative alternative, but one that gives good results.
The Woodward-Hoffmann theory tries to see how reactants are transformed into products, and tries to predict that when in the formation of reactants to products the energy barrier is large then the reaction will be forbidden. Whereas if that transformation takes place without a large energy barrier, then it will be allowed. Furthermore, they proposed that in order for the reactants to be transformed into products, the correlating orbitals have to maintain the orbital symmetry of the system, i.e., when going from reactants to products the symmetry of the system has to be maintained. The implementation of this correlation between reactants and products is called correlation diagrams.
First we will look at a more qualitative aspect, bearing in mind that in all pericyclic reactions a transition state is produced which is fundamentally constituted by a series of electrons interacting in a closed loop and bearing in mind that this reminds us of aromatic systems where in addition to the σ chain, there are π electrons in a closed loop. The number of electrons and their topology implies the aromaticity or antiaromaticity of closed cyclic hydrocarbons. The point of view of Dewar and Zimmerman, who developed this alternative, is to make an analogy between the transition state and the aromaticity or anti-aromaticity of polycyclic polyunsaturated hydrocarbons, so that if in this analogy the transition state can be assigned an aromatic character, this transition state will be stabilized and therefore the reaction will be allowed. Whereas if in this analogy the transition state can be assigned an antiaromatic character, then the transition state will be destabilized and the reaction will be forbidden. It is then a matter of constructing an approximate transition state representing the interacting electron pairs in the pericyclic reaction and trying to assign it an aromatic or antiaromaticcharacter.
Diagramas de interacción de orbitales
To perform the qualitative construction of this transition state, interaction diagrams are used, i.e., the transition states of pericyclic reactions are constructed by means of these diagrams, which are a representation of the interaction of the orbitals involved in the pericyclic reaction.
Some of this we have already seen by looking at a cycloaddition reaction where we have put a π system of 2 electrons and another of 4 electrons, we have said that an attack from above must take place so that that interacts supra–supra.

But this is only a partial interaction between the components involved.
Supra or antara interaction
Before arriving between the types of interaction between the components involved, which are the ones that set the stereochemistry of the reaction in order to analyze the interaction diagram as a whole, it is necessary to analyze also the interaction within each component. That is, we have to study the interaction existing in a π system, within a σ orbital, etc. For example, if we have a π system of 2 electrons, it can interact with another one supra or antarafacialmente, but in that π system of 2 electrons, in the transition state there is an interaction between those two orbitals with each other in a way that has to be suprafacial.
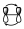
Or, in a 4-electron π system, the interaction within those orbitals will be as shown:
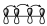
This indicates that there is no interaction between the ends, but there is interaction within the lobes of each of them. Logically, these interaction diagrams for this dienic system must be equivalent to this one.
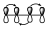
Since the interaction of 2 lobes above is equivalent to the interaction of these below. It should be noted that we are not looking at the sign of the different lobes, but these two diagrams must be equivalent when analyzing the interaction within a π system.
The same as if we have an s orbital we have seen that it can interact with other components in a supra or antara way, if it does so supra the two lobes of the same sign interact with each other, and vice versa. But the interaction between them logically is in this way, since they form the bond

So, that will be the interaction inside a σ bond. But if we look at any reaction where a system is involved, normally that σ system becomes a π system, in the transition state a change of sp3 hybridization to a p orbital is taking place, and therefore it is neither one thing nor the other, so the above is equivalent to the interaction between 2 p orbitals.

That is to say, that normally in the interaction diagrams the shape of the orbitals that are part of it is not taken into account, it is not taken into account if it is a σ orbital, if there are sp3 or sp2 hybrids, etc, but only the base orbitals that will represent the interaction within the system are considered. A σ orbital can be represented identically by an interaction of a π system with two p orbitals, because in reality in the transition state the first is evolving to the second and what we will have will be something intermediate, therefore within the interaction diagram both are totally equivalent.
To make the interaction diagram, although we have said that the interactions from above and below are equivalent, normally what is done is to take the interactions in such a way that they are always on the same side, provided that this corresponds to the topology of the molecule. Then before starting to study the interaction between components, what we do is within each component to study its interaction, so that the interaction always occurs on the same side of the π system, and also taking into account that a σ system becomes equivalent to the interaction of 2 orbitals.
If in a pericyclic reaction a transition state is postulated in which a closed loop of interacting orbitals can be found, then it is logical to think that if this loop has a structure somewhat reminiscent of those of aromatic systems, this transition state will be stabilized and therefore the reaction will occur in preference to another that is destabilized, because it resembles an antiaromatic system. In this process of construction of transition state and its study to see if they can be associated with aromatic or antiaromatic character, what is done is the construction of interaction diagrams.
We have seen how the interaction can be defined within the base orbitals of a system involved in the reaction. Thus in a linear π-system, interaction can be established, before performing the reaction, between the lobes on the same side with respect to each other, etc.
Since we can know the interaction that exists within the systems that will intervene in the reaction, we will see how the reaction is defined in the course of the reaction. It must be taken into account that this interaction must represent the topology of the reaction, therefore it must give rise to different interaction diagrams with different topologies. Taking into account that in the course of the reaction the π and σ orbitals are transformed in such a way that in the TS they are intermediate situations, that is why the interaction diagram can be transformed from a σ interaction to two p orbitals. The same can be said with respect to the complete interaction diagram of the whole reaction, what it is about is to reproduce the topology of the reaction taking into account that in the TS the σ orbitals are not σ nor the π are π, but something intermediate, and the important thing is that it reproduces the topology of how the reactants are transformed into the products passing through the transition state.
Example of application in Diels-Alder reaction [4+2]
Let’s give some examples in order to establish some criteria to draw these interaction diagrams in a simple way. Let us assume a π2+π4 cycloaddition reaction such as the Diels-Alder reaction.
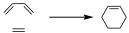
Before the reaction takes place, we can define the interaction within the lobes of the 4-electron π-system and the 2-electron π-system.

Now, we can say that that is a reaction in which there is an attack of a dienic system on an ethylenic system to give rise to a 6-membered cyclic system. That interaction can be supra–supra or supra–antara. The Diels-Alder reaction is supra–supra, therefore an interaction will occur as drawn. From the interaction for this reaction, i.e., the representation of the transition state, we can represent it in this way, taking into account that it does not matter whether we put the interaction above or below, both are fully equivalent.

What is important is that there is an interaction of one party with the other, so that the interaction occurs supra–supra.
This interaction diagram can be made from both the direct cycloaddition reaction and the cycloreversion reaction. Let us see how the same diagram is obtained for the cycloreversion reaction. In the cycloreversion we have the π system and 2 σ systems involved, i.e., in a cycloreversion it would be a π2+σ2+σ2 reaction. So the interaction diagram before the reaction takes place would be, taking into account that the σ systems are equivalent to the π orbitals.

These three interaction diagrams are equivalent, because in both cases we have a supra–supra interaction. the interaction diagram has to represent the type of interaction that occurs.
Ejemplo de interacción en cicloadición [2+2]
Another example of supra–supra interaction is the following π2+π2:

Now let’s look at a supra–antara interaction, let’s see that it gives rise to a totally different topology. Let’s assume a π2s+π2a interaction, the interaction of the base orbitals before giving rise to the reaction.

These interaction diagrams are different from the previous ones, there is no way to transform one into the other and therefore involve two different topologies.
The orientation so that the supra-antara interaction can occur will be as follows, where one of the systems is oriented in such a way that one of the π systems is oriented in a plane perpendicular to the plane of the paper with the orbital p in the plane of the paper. The other system is oriented in a perpendicular direction so that we have the π system oriented in a plane perpendicular to the plane of the paper and therefore the substituents are in the plane of the paper.
These interaction diagrams are different from the previous ones, there is no way to transform one into the other and therefore involve two different topologies.

So the component that is vertical acts supra-facially, because there is going to be interaction with the two lobes going inwards. But interaction can occur above and below the other component that is in the perpendicular direction in such a way that this interaction is produced and curved in such a way that there is a twisting that implies a change in the configuration of one of the components that acts antarfacially. This implies a different topology from the parallel approach of the two systems p that gives rise to the other interaction diagram.
Example of interaction in sigmatropic transposition[1,3]
We have drawn some interaction diagrams but not complete ones, since we have not said anything about the signs of the lobes, nor how aromatic or antiaromatic character is assigned to these interaction diagrams. We will first look at some examples of pericyclic interactions where the interaction diagram can be easily extracted.
Let us assume a sigmatropic transposition reaction [1,3]. Where we have a π system and a σ orbital which is going to transpose from position 1 to position 3. This reaction can occur in two ways, one in which a supra-supra interaction takes place and one in which it is supra of the π system and antara of the migrating σ group. For a supra-antara interaction to occur it has to be of this type, where the representation of the transition state would be:

All the reaction with a supra-antara interaction with the same number of electrons has to have the same interaction diagram.
Example of interaction in electrocyclic reaction
Let us look at an example of electrocyclic reactions, for example conrotatory or disrotatory opening. If the opening is conrotatory, the interaction is supra–antara and must give an interaction diagram similar to the one we have seen before to the sigmatropic transposition reaction or to the π2s+π2a cycloaddition.

We have already seen that the conrotatory opening implies a π2a+σ2s cycloaddition.
The disrotatory pulls in a conrotatory direction and therefore one lobe goes upward and the other one goes upward as well.

Which is fully equivalent to a π2s+π2s cycloaddition. Thus in general, we will be able to draw any interaction diagram of any of the reactions we have said so far. Simply by taking into account the topology of the reaction and the supra or antarainteractions that occur in the various components or base orbitals involved in the reaction.
Aromatic/antiaromatic character in interaction diagrams
Once we know how to construct the interaction diagram, let’s see how to assign the aromatic or antiaromatic characters to these diagrams, for which we have to put signs to the lobes of the p orbitals that integrate the interaction diagram. The rule that is followed is + for the lobes that are joined by interaction lines whenever possible.

We see how in the second case we cannot assign the sign + to all the joined lobes. Thus we see how the topology of the interaction diagram implies that all interactions are between positive lobes in the first case while in the second case they occur between lobes that have different signs.
But in general the assignment of signs can be done randomly, for example, in the first case above.
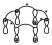
Phase inversion
When the signs are assigned, a phase inversion is said to occur if there is an interaction between lobes of different signs. In that diagram there will therefore be 4 phase inversions. In the case of the previous 2, in the first case there were zero phase inversions and in the second case there was one.
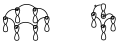
If in one of these diagrams we change any sign of place, in the first case, when changing signs of place randomly, an even number of phase inversions appear, while in the second case, an odd number of phase inversions appear.

In general, when there is a supra–supra topology between all the components, interaction diagrams with an even number (or zero) of phase inversions are obtained. While when the interaction is supra–antara these diagrams have an odd number of phase inversions or at least one. We can always reduce the interaction diagrams to the minimum number of phase inversions (0 or 1).
We are now in a position to define whether an interaction diagram will be aromatic or antiaromatic, by analogy to conjugated systems. Thus, in benzene and cyclobutadiene we have:

For benzene we have 6 electrons and the interaction there is one in which all the lobes above interact with each other (with 0 phase reversals). In the case of cyclobutadiene it can also be represented as a supra–supra interaction with 4 electrons. Then systems with electron number π = 4n+2 (n=1, 2, 3, …) are aromatic, and conjugated cyclic (saturated) systems with electron number π = 2n are antiaromatic. But both respond to interaction diagrams with zero phase reversal. Aromatic systems are stabilized against non-cyclic conjugated systems while antiaromatic systems are destabilized.
Hückel and Möbius systems
There are large conjugated systems in which there is a twisting in the chain by means of what are called Möbius belts. However, we can represent an aromatic system as a circle in which there is always an interaction from above and below. Whereas in a Möbius system there is a folding in such a way that the upper part ends up interacting with the lower part.

This causes the aromatic or antiaromatic character in a polycyclic system to change. In a Möbius system the aromatic character is associated with a number of electrons equal to 4n, while the antiaromatic character is associated with a number of electrons equal to 4n+2. In addition, the interaction involves a phase reversal because folding occurs. That said, we can assign the aromatic or antiaromatic character to the interaction diagrams. We will therefore divide them into two groups:
Interaction diagrams with 0 phase inversion
They are known as Hückel-type rings. In these diagrams an aromatic character is assigned to those with a number of electrons equal to 4n+2, those with 4n are assigned an antiaromatic character. The former are favored over the latter, in them the transition state will be stabilized, therefore the former will occur more easily. It is said that those with aromatic character are allowed, while those with antiaromatic character are forbidden (it does not mean that they cannot occur, but that there is a very large energy barrier in the transition state, but under special conditions the forbidden one could occur and not the allowed one (e.g. steric interactions).
Interaction diagrams with 1 phase inversion
Anti-Hückel type rings or anti-Hückel type interaction diagrams are also defined as those that have a phase inversion. In these cases, aromatic character is associated to those interaction diagrams that have a number of electrons equal to 4n, while those with a number 4n+2 will be antiaromatic.
So to predict whether a reaction will occur or not, it boils down to constructing the interaction diagram, once we do that we see if it corresponds to one or zero phase reversals, we see the number of electrons in the diagram and we can tell if it is allowed or forbidden.
Let us assume electrocyclic reactions, where the opening of that σ orbital (or closure, since it is a reversible reaction) occurs to give rise to the corresponding triene. The opening as we know can be conrotatory or disrotatory.

If it is disrotatory, we will have on the one hand the π system of 4 electrons interacting with the s system of two electrons, so that the s system will open upwards the two so that the interaction will occur above and we will have a supra–suprainteraction, which implies zero phase reversals and as there are 6 electrons it will be an aromatic system and that reaction will be allowed. The electrocyclic opening with 6 electrons will be allowed if it is dystrophic:

In the conrotatory one, on the other hand, one lobe turns upwards and the other downwards, so the interaction will occur with a phase inversion, it will be an anti-Hückel ring and therefore the reaction will be forbidden since it is an antiaromatic system.

This implies that the latter transition state has a much higher activation energy than the former and the reaction will preferentially proceed along the former path.
Let us now look at other approaches, since what we want is to predict when a reaction will occur and with what stereochemistry.
Interacciones de orbitales frontera
This approach was proposed by Woodward-Hoffmann and further developed by Fukui. The HOMO and LUMO are called boundary orbitals.
According to perturbation theory, for an interaction to take place as favorably as possible, it has to take place between a full and an empty orbital, and furthermore, for the two orbitals to have the most favorable energy content possible. This is something that is fulfilled with the boundary orbitals. Since if we have a series of orbitals, in principle, any occupied orbital could interact with an empty one, but the large energy difference between them will be very large. However, the difference is small when the last of the occupied (HOMO) interacts with the first of the unoccupied (LUMO). These will be the preferred conditions for the best possible interaction between orbitals.
In addition, Woodward-Hoffmann proposed that for an interaction to occur between two orbitals they must have the same symmetry. Therefore, of all the possibilities, only those with the same symmetry between the interacting orbitals will be given. In this way, the different pericyclic reactions can be rationalized.
Example of [2+2] cycloaddition
For example, suppose a π2 + π2 cycloaddition. In this reaction we can have two symmetry elements, let us consider the symmetry element bisecting both systems (σ plane). With respect to that plane the orbitals of the interacting systems are considered. On the one hand in one of the systems we have the bonding π orbital and another π*, and the same for the other system.

The symmetry is taken with respect to that plane. If now the interaction has to take place between the LUMO of one and the HOMO of the other, but since they do not have proper symmetry, that reaction will be symmetry forbidden. The only possibility is that interaction occurs between the two HOMOs or the two LUMOs. The first one gives rise to two occupied orbitals and this is a destabilizing situation and the second one gives rise to two virtual vacuums which is therefore useless.
Example of [4+2] cycloaddition
If we now consider a π4 + π2 cycloaddition. In the π4 system we will have four orbitals of which the first two are occupied and the next two are virtual, the symmetry with respect to the same plane which remains the symmetry element will be:

As can be seen, now the interaction between the ethylene HOMO and the butadiene LUMO can be established, giving rise to a stabilizing interaction since the lowest energy orbital is populated. It can also occur between the butadiene HOMO and the ethylene LUMO where the lowest energy orbital is also populated. Therefore, two equally stabilizing interactions can occur (although they will not be very stabilizing since the overlap is small, but enough to produce a decrease in energy).
The normal thing is that the dienic system has an electron donor substituent and the ethylenic system an electron attractor, with this the only thing that is achieved is that the energy differences are identical for both interactions, one of them is very stabilized against the other even if only one interaction occurs between the HOMO of the giver with the LUMO of the acceptor, of the two possible interactions that can occur.