Introduction
Before beginning to understand Nuclear Magnetic Resonance (NMR) spectroscopy, we must consider the properties of atomic nuclei that cause this phenomenon to appear.
Properties of atomic nuclei
The nuclei have two types of remarkable properties:
- Mechanical properties: which we can imagine assuming a planetary simile: The angular momentum which is due to the motion of the nuclei around a given point and the nuclear spin (I) which is due to the rotational motion of the nuclei and depends on the charge/mass ratio of the nuclei.
- Electrical properties: among which are the electrical charge. Also, a magnetic momentum (μ) caused by the rotational motion of any electrically charged body. And a Quadrupole moment, due to the non-uniform distribution of a charge on a surface and which appears when the nucleus is not absolutely spherical.
When we consider a sample consisting of many nuclei, the moments of these nuclei will have a random distribution.

However, if we subject such nuclei to a magnetic field they will tend to orient themselves in it. Thus, let us imagine that the nuclei are similar to small magnets (see Figure). Then, they will have two possible states: either aligned with it (state α, more stable or lower energy), or opposite to it (state β, less stable or higher energy).
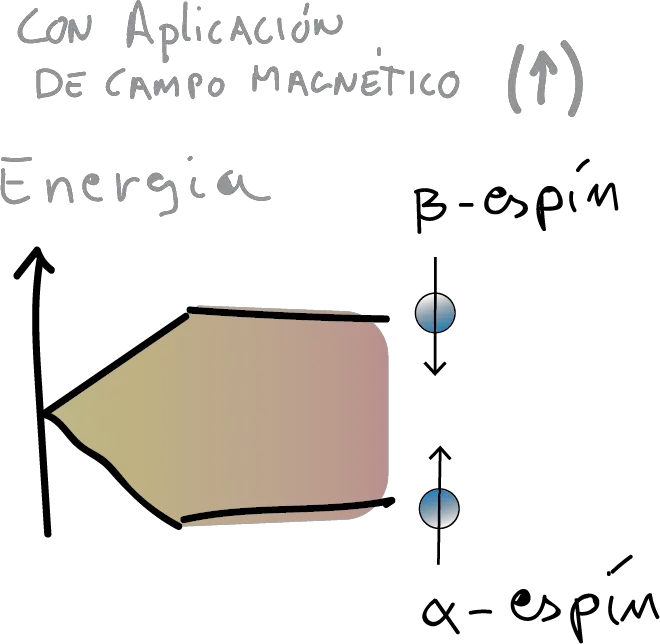
In reality, it is not that the magnetic moments are aligned with the magnetic field. Rather, they precess or rotate (as if they were a spinning top) around the direction marked by it. Moreover, they do so not with any speed but with a speed that depends on the nature of the nucleus and the strength of the field.
This is quantified by the Equation of Larmor, which can be expressed in different ways:
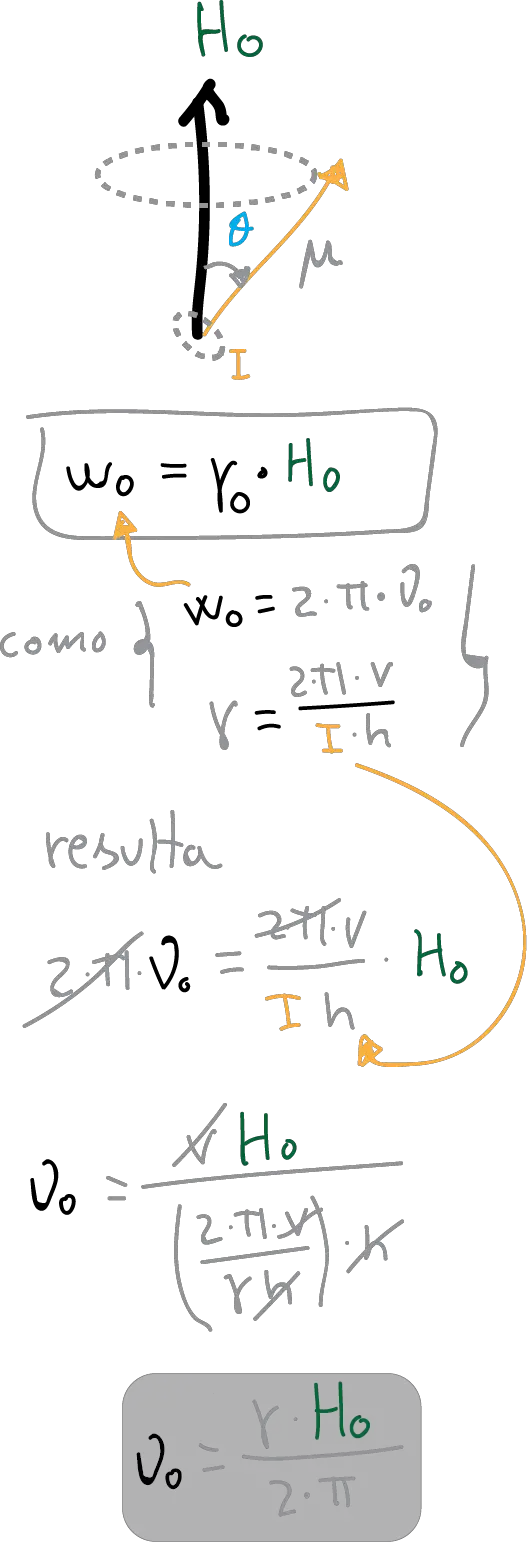
in this expression h-νo has units of energy and would be equivalent to say that when the nucleus is subjected to a magnetic field Ho, an absorption of energy occurs when the frequency of the radiation is equal to νo, at which time it is said to be in resonance.
This energy happens to be in the radiofrequency zone: νo in MHz (106 Hz) and depends on the intensity of the applied field, Ho. Thus for Hydrogen-1 at a field Ho of 14000 Gauss (1.40 Teslas), the resonance frequency would be 60 MHz, which is equivalent to an energy of 0.0057 cal/mol.
Resonance frequency
Two questions immediately arise:
- Do all nuclei have a characteristic resonance signal or is it the same for all nuclei?
- If not, is its frequency of the same order of magnitude?
The answer to the first question is NO, not all nuclei will have a characteristic resonance frequency when subjected to a magnetic field, only those that have either the atomic number, the mass number, or both with an odd value will have it.
Those with both pairs will not have a resonance signal, as shown in Table 1:
| Mass nº (Atomic nº) | Signal NMR | Examples |
| Even (even) | ✘ | 12C6 , 16O8 |
| Even (odd) |  | 2H1, 10B5, 14N7 |
| Odd (even) |  | 13C6, 17O8 |
| Odd (odd) |  | 1H1, 11B5, 15N7 |
The answer to the second question is YES, all those nuclei that meet the above condition possess a characteristic NMR signal when subjected to a magnetic field (Ho).
Therefore, the frequency of such a signal will depend on the physical characteristics of the nucleus in question and the relative sensitivity will depend on the natural abundance of that nucleus.
In Table 2 the most common nuclei and their resonance frequencies at 10000 Gauss are shown:
| Nucleus | Natural abundance (%) | Spin | Magnetic moment (mag.nuc) | NMR frequency (MHz)* | Relative sensitivity | Cte. γ 108 (SI) |
|---|---|---|---|---|---|---|
| 1H1 | 99.9844 | 1/2 | 2.79268 | 42.5759 | 1.000 | 2.6752 |
| 2H1 | 0.0156 | 1 | 0.857386 | 6.53566 | 0.00964 | 0.4107 |
| 7Li3 | 92.57 | 3/2 | 3.2560 | 16.547 | ||
| 9Be4 | 100 | 3/2 | -1.1773 | 5.983 | ||
| 10B5 | 18.83 | 3 | 1.8005 | 4.575 | 0.0199 | 0.2875 |
| 11B5 | 81.17 | 3/2 | 2.6880 | 13.660 | 0.165 | 0.8583 |
| 13C6 | 1.108 | 1/2 | 0.70220 | 10.705 | 0.159 | 0.6726 |
| 14N7 | 99.635 | 1 | 0.40358 | 3.076 | 0.00101 | 0.1933 |
| 15N7 | 0.365 | 1/2 | -0.28304 | 4.315 | 0.00104 | -0.271 |
| 17O8 | 0.037 | 5/2 | -1.8930 | 5.772 | ||
| 19F9 | 100 | 1/2 | 2.6273 | 40.055 | 0.834 | 2.5167 |
| 23Na11 | 100 | 3/2 | 2.2161 | 11.262 | ||
| 25Mg12 | 10.05 | 5/2 | -0.85471 | 2.606 | ||
| 27Al13 | 100 | 5/2 | 3.6385 | 11.094 | ||
| 29Si14 | 4.70 | 1/2 | -0.55477 | 8.458 | 0.0785 | -0.532 |
| 31P15 | 100 | 1/2 | 1.1305 | 17.236 | 0.0664 | 1.0829 |
| 33S16 | 0.74 | 3/2 | 0.64274 | 3.266 | ||
| 35Cl17 | 75.4 | 3/2 | 0.82091 | 4.172 | ||
| 37Cl17 | 246 | 3/2 | 0.68330 | 3.472 | ||
| 39K19 | 93.08 | 3/2 | 0.39094 | 1.987 | ||
| 79Br | 50.57 | 3/2 | 2.0991 | 10.667 | ||
| 81Br | 49.43 | 3/2 | 2.2626 | 11.499 | ||
| e- | - | 1/2 | -1836 | 28024.6 |
From the data in Table 2, we should highlight the resonance frequency and spin number (both columns in red). In addition, in blue those nuclei most useful for organic chemists. That is: C, H, F and P, and of them really useful are only 1H and 13C (and this one with the limitation of being the minority isotope of carbon and therefore having a small sensitivity). F and P appear only sporadically in organic compounds.
Usefulness of NMR
But it is worth asking about the usefulness of NMR, since so far this technique has only been used to perform a kind of elemental isotope analysis of a sample, as for example shown in the spectrum of a water sample contained in a borosilicate tube in the following figure:
fig-3
An additional issue, independent of the “possible usefulness of the technique“, is the question of the sensitivity of the technique. As discussed previously the energy involved in the resonance experiment is very small (in the thousandths of cal/mol range).
Therefore, the population difference between the two energy levels involved in that absorption will be very small: for a Hoof 9400 Gauss and at room temperature, the population ratio between both levels according to the Boltzmann equation will be:
In short, this indicates that out of every two million nuclei only 6 of them would absorb radiation. In order to increase this sensitivity somewhat, strong magnetic fields are used, because the higher the Ho the higher the resonance frequency (and therefore the energy difference) and also the difference in populations between the spin states:
fig-4
Obtaining an NMR spectrum
The next question to ask is how to obtain a nuclear magnetic resonance spectrum of a sample?
To do this we will first need a sample contained in a container, usually a glass tube of certain qualities and characteristics. Next, we will need a magnetic field in which to introduce the sample, i.e. a magnet. Thus, the first magnets were conventional magnets (a soft iron core and a coil wound around it). But since the mid-1960s, superconductors have been used, which are easier to manufacture and achieve much stronger fields. Next, since the energy absorption in NMR corresponds to the wavelength of radiofrequencies, we need a radiofrequency emitter with which to irradiate the sample. In addition, in order to observe whether absorption has occurred, we will also need a radiofrequency receiver and a detector to compare these radiations. Finally, we will need a computer to convert the observed waves into an interpretable NMR spectrum.